
已知数列 满足
满足
(1)求证:数列 的奇数项,偶数项均构成等差数列;
的奇数项,偶数项均构成等差数列;
(2)求 的通项公式;
的通项公式;
(3)设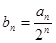 ,求数列
,求数列 的前
的前 项和
项和 .
.
科目:高中数学 来源:2014届湖北省荆门市高一下学期期末质量检测数学试卷(解析版) 题型:解答题
已知数列 满足
满足
(1) 求证:数列 的奇数项,偶数项均构成等差数列;
的奇数项,偶数项均构成等差数列;
(2) 求 的通项公式;
的通项公式;
(3) 设 ,求数列
,求数列 的前
的前 项和
项和 .
.
查看答案和解析>>
科目:高中数学 来源:2013届安徽无为开城中学高二下学期期末考试理科数学试卷(解析版) 题型:解答题
已知数列 满足
满足 =-1,
=-1, ,数列
,数列 满足
满足
(1)求证:数列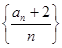 为等比数列,并求数列
为等比数列,并求数列 的通项公式.
的通项公式.
(2)求证:当 时,
时,
(3)设数列 的前
的前 项和为
项和为 ,求证:当
,求证:当 时,
时, .
.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省南京市、盐城市高三第一次模拟考试数学(解析版) 题型:解答题
(本小题满分16分) [已知数列 满足
满足
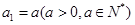 ,
,
 .
.
(1)求数列 的通项公式
的通项公式 ;
;
(2)若对每一个正整数 ,若将
,若将 按从小到大的顺序排列后,此三项均能构成等
按从小到大的顺序排列后,此三项均能构成等
差数列, 且公差为 .①求
.①求 的值及对应的数列
的值及对应的数列 .
.
②记 为数列
为数列 的前
的前 项和,问是否存在
项和,问是否存在 ,使得
,使得 对任意正整数
对任意正整数 恒成立?若存
恒成立?若存
在,求出 的最大值;若不存在,请说明理由.
的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省高三下学期期末考试数学试卷 题型:解答题
(本小题满分16分)
已知数列 满足
满足 ,(1)若
,(1)若 ,求
,求 ;
;
(2)是否存在 ,使当
,使当 时,
时, 恒为常数。若存在求
恒为常数。若存在求 ,否则说明理由;
,否则说明理由;
(3)若 ,求
,求 的前
的前 项的和
项的和 (用
(用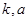 表示)
表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com