
【题目】若圆经过点(2,0),(0,4),(0,2)求:
(1)圆的方程
(2)圆的圆心和半径.
【答案】
(1)解:设圆的一般式为x2+y2+Dx+Ey+F=0,
将已知三点代入方程得:
 ,
,
解得 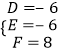 ;
;
所以圆的方程为x2+y2﹣6x﹣6y+8=0
(2)解:因为圆的方程为x2+y2﹣6x﹣6y+8=0,
所以﹣ ![]() =3,﹣
=3,﹣ ![]() =3,
=3,
即圆心坐标为(3,3);
所以圆的半径为:
r= ![]() =
= ![]()
![]() =
= ![]()
【解析】(1)设出圆的一般式,把三点坐标代入方程即可求出圆的方程;(2)利用圆的方程求出圆心与半径即可.
【考点精析】关于本题考查的圆的一般方程,需要了解圆的一般方程的特点:(1)①x2和y2的系数相同,不等于0.②没有xy这样的二次项;(2)圆的一般方程中有三个特定的系数D、E、F,因之只要求出这三个系数,圆的方程就确定了;(3)、与圆的标准方程相比较,它是一种特殊的二元二次方程,代数特征明显,圆的标准方程则指出了圆心坐标与半径大小,几何特征较明显才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】双流中学2016年高中毕业的大一学生假期参加社会实践活动,为提高某套丛书的销量,准备举办一场展销会,据市场调查,当每套丛书售价定为![]() 元时,销售量可达到
元时,销售量可达到![]() 万套,现出版社为配合该书商的活动,决定进行价格改革,将每套丛书的供货价格分成固定价格和浮动价格两部分,其中固定价格为30元,浮动价格(单位:元)与销售量(单位:万套)成反比,比例系数为10,假设不计其他成本,即销售每套丛书的利润=售价
万套,现出版社为配合该书商的活动,决定进行价格改革,将每套丛书的供货价格分成固定价格和浮动价格两部分,其中固定价格为30元,浮动价格(单位:元)与销售量(单位:万套)成反比,比例系数为10,假设不计其他成本,即销售每套丛书的利润=售价![]() 供货价格.问:
供货价格.问:
(1)每套丛书售价定为100元时,书商所获得的总利润是多少万元?
(2)每套丛书售价定为多少元时,单套丛书的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且满足 ![]() acosC﹣csinA=0.
acosC﹣csinA=0.
(1)求角C的大小;
(2)已知b=4,△ABC的面积为6 ![]() ,求边长c的值.
,求边长c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定椭圆C: ![]() (a>b>0).称圆心在原点O,半径为
(a>b>0).称圆心在原点O,半径为 ![]() 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为F(
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为F( ![]() ,0),其短轴上的一个端点到点F的距离为
,0),其短轴上的一个端点到点F的距离为 ![]() .
.
(1)求椭圆C的方程和其“准圆”方程;
(2)点P是椭圆C的“准圆”上的一个动点,过动点P作直线l1 , l2 , 使得l1 , l2与椭圆C都只有一个交点,试判断l1 , l2是否垂直,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产的产品在出厂前都要做质量检测,每件一等品都能通过检测,每件二等品通过检测的概率为![]() .现有
.现有![]() 件产品,其中
件产品,其中![]() 件是一等品,
件是一等品, ![]() 件是二等品.
件是二等品.
(Ⅰ)随机选取![]() 件产品,设至少有一件通过检测为事件
件产品,设至少有一件通过检测为事件![]() ,求事件
,求事件![]() 的概率;
的概率;
(Ⅱ)随机选取![]() 件产品,其中一等品的件数记为
件产品,其中一等品的件数记为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com