
【题目】设椭圆 ![]() =1(a>b>0)的左焦点为F,离心率为
=1(a>b>0)的左焦点为F,离心率为 ![]() ,过点F且与x轴垂直的直线被椭圆截得的线段长为
,过点F且与x轴垂直的直线被椭圆截得的线段长为 ![]() .
.
(1)求椭圆的方程;
(2)设A,B分别为椭圆的左,右顶点,过点F且斜率为k的直线与椭圆交于C,D两点.若 ![]() =8,求k的值.
=8,求k的值.
【答案】
(1)解:根据椭圆方程为 ![]() .
.
∵过焦点且垂直于x轴的直线被椭圆截得的线段长为 ![]() ,
,
∴当x=﹣c时, ![]() ,得y=±
,得y=± ![]() ,
,
∴ ![]() =
= ![]() ,
,
∵离心率为 ![]() ,∴
,∴ ![]() =
= ![]() ,
,
解得b= ![]() ,c=1,a=
,c=1,a= ![]() .
.
∴椭圆的方程为 ![]() ;
;
(2)解:直线CD:y=k(x+1),
设C(x1,y1),D(x2,y2),
由 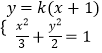 消去y得,(2+3k2)x2+6k2x+3k2﹣6=0,
消去y得,(2+3k2)x2+6k2x+3k2﹣6=0,
∴x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() ,又A(﹣
,又A(﹣ ![]() ,0),B(
,0),B( ![]() ,0),
,0),
∴ ![]()
=(x1+ ![]() ,y1)(
,y1)( ![]() ﹣x2.﹣y2)+(x2+
﹣x2.﹣y2)+(x2+ ![]() ,y2)(
,y2)( ![]() ﹣x1.﹣y1),
﹣x1.﹣y1),
=6﹣(2+2k2)x1x2﹣2k2(x1+x2)﹣2k2,
=6+ ![]() =8,解得k=
=8,解得k= ![]() .
.
【解析】(1)先根据椭圆方程的一般形式,令x=c代入求出弦长使其等于 ![]() ,再由离心率为
,再由离心率为 ![]() ,可求出a,b,c的关系,进而得到椭圆的方程.(2)直线CD:y=k(x+1),设C(x1 , y1),D(x2 , y2),由
,可求出a,b,c的关系,进而得到椭圆的方程.(2)直线CD:y=k(x+1),设C(x1 , y1),D(x2 , y2),由 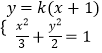 消去y得,(2+3k2)x2+6k2x+3k2﹣6=0,再由韦达定理进行求解.求得
消去y得,(2+3k2)x2+6k2x+3k2﹣6=0,再由韦达定理进行求解.求得 ![]() ,利用
,利用 ![]() =8,即可求得k的值.
=8,即可求得k的值.
【考点精析】利用一般式方程和椭圆的标准方程对题目进行判断即可得到答案,需要熟知直线的一般式方程:关于![]() 的二元一次方程
的二元一次方程![]() (A,B不同时为0);椭圆标准方程焦点在x轴:
(A,B不同时为0);椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.


 互动英语系列答案
互动英语系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)满足:①对任意x∈(0,+∞),恒有f(2x)=2f(x)成立;②当x∈(1,2]时,f(x)=2﹣x.若f(a)=f(2020),则满足条件的最小的正实数a的值为( )
A. 28 B. 100 C. 34 D. 36
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若将函数y=2sin 2x的图像向左平移 ![]() 个单位长度,则评议后图象的对称轴为( )
个单位长度,则评议后图象的对称轴为( )
A.x= ![]() –
– ![]() (k∈Z)
(k∈Z)
B.x= ![]() +
+ ![]() (k∈Z)
(k∈Z)
C.x= ![]() –
– ![]() (k∈Z)
(k∈Z)
D.x= ![]() +
+ ![]() (k∈Z)
(k∈Z)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖冲之之子祖暅是我国南北朝时代伟大的科学家,他在实践的基础上提出了体积计算的原理:“幂势既同,则积不容异”.意思是,如果两个等高的几何体 在同高处截得的截面面积恒等,那么这两个几何体的体积相等.此即祖暅原理.利用这个原理求球的体积时,需要构造一个满足条件的几何体,已知该几何体三视图 如图所示,用一个与该几何体的下底面平行相距为 h(0<h<2) 的平面截该几何体,则截面面积为 ( )
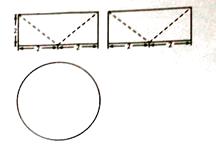
A.![]()
B.![]()
C.![]()
D.π(4-h2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已成椭圆 ![]() 的左右顶点分别为
的左右顶点分别为 ![]() ,上下顶点分别为
,上下顶点分别为 ![]() ,左右焦点分别为
,左右焦点分别为 ![]() ,其中长轴长为4,且圆
,其中长轴长为4,且圆 ![]() 为菱形
为菱形 ![]() 的内切圆.
的内切圆.
(1)求椭圆 ![]() 的方程;
的方程;
(2)点 ![]() 为
为 ![]() 轴正半轴上一点,过点
轴正半轴上一点,过点 ![]() 作椭圆
作椭圆 ![]() 的切线
的切线 ![]() ,记右焦点
,记右焦点 ![]() 在
在 ![]() 上的射影为
上的射影为 ![]() ,若
,若 ![]() 的面积不小于
的面积不小于 ![]() ,求
,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在考试测评中,常用难度曲线图来检测题目的质量,一般来说,全卷得分高的学生,在某道题目上的答对率也应较高,如果是某次数学测试压轴题的第1、2问得分难度曲线图,第1、2问满分均为6分,图中横坐标为分数段,纵坐标为该分数段的全体考生在第1、2问的平均难度,则下列说法正确的是( ) 
A.此题没有考生得12分
B.此题第1问比第2问更能区分学生数学成绩的好与坏
C.分数在[40,50)的考生此大题的平均得分大约为4.8分
D.全体考生第1问的得分标准差小于第2问的得分标准差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的离心率为
的离心率为 ![]() ,M为C上除长轴顶点外的一动点,以M为圆心,
,M为C上除长轴顶点外的一动点,以M为圆心, ![]() 为半径作圆,过原点O作圆M的两条切线,A、B为切点,当M为短轴顶点时∠AOB=
为半径作圆,过原点O作圆M的两条切线,A、B为切点,当M为短轴顶点时∠AOB= ![]() . (Ⅰ)求椭圆的方程;
. (Ⅰ)求椭圆的方程;
(Ⅱ)设椭圆的右焦点为F,过点F作MF的垂线交直线x= ![]() a于N点,判断直线MN与椭圆的位置关系.
a于N点,判断直线MN与椭圆的位置关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com