练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某公司的生产部门调研发现,该公司第二、三季度的月用电量与月份线性相关,且数据统计如下表:

    但核对电费报表时发现一组数据统计有误.

    (1)请指出哪组数据有误,并说明理由;

    (2)在排除有误数据后,求月用电量与月份之间的回归方程,并预测统计有误月份的用电量.(结果精确到0.1)

    附注:,

    【答案】（1）见解析；（2）36.2

    【解析】

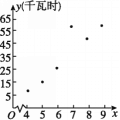
    （1散点图如图所示，因为供水量与月份线性相关，点（7，55）离其它点所在区域较远，故（7，55）有误；

    （2）求出=6.4，=30.2，可得b，a，可得用电量与月份之间的回归直线方程=x+，x=7时，即可预测统计有误那个月份的用电量．

    (1)作散点图如图所示.因为用电量与月份之间线性相关,所以散点图的样本点分布在回归直线附近比较窄的带状区域内,而点(7,55)离其他点所在区域较远,故(7,55)这组数据有误.

    (2)排除(7,55)这一组有误数据后,计算得=6.4，=30.2.

    因为b=≈9.98, a=30.2﹣9.98×6.4=﹣33.67，,

    ∴y=9.98x﹣33.67，

    x=7时，y=9.98×7﹣33.67=36.2

    即7月份的用电量大约为36.2千瓦时.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】A、B两个投资项目的利润率分别为随机变量X1和X2，根据市场分析，X1和X2的分布列分别为

    X1

    5%

    10%

    P

    0.8

    0.2

    X2

    2%

    8%

    12%

    P

    0.2

    0.5

    0.3

    (1)在A，B两个项目上各投资100万元，Y1和Y2分别表示投资项目A和B所获得的利润，求方差V(Y1)、V(Y2)；

    (2)将x(0≤x≤100)万元投资A项目，100－x万元投资B项目，f(x)表示投资A项目所得利润的方差与投资B项目所得利润的方差的和．求f(x)的最小值，并指出x为何值时，f(x)取到最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设、为曲线：上两点，与的横坐标之和为．

    （1）求直线的斜率；

    （2）为曲线上一点，在处的切线与直线平行，且，求直线的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列语句中是命题的有________,其中是真命题的有_____(填序号).

    ①“垂直于同一条直线的两个平面必平行吗?”②“一个数不是正数就是负数”;③“在一个三角形中,大角所对的边大于小角所对的边”;④“若x+y为有理数,则x,y都是有理数”;⑤作一个三角形.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x2﹣ax+b（a＞0，b＞0）有两个不同的零点m，n，且m，n和﹣2三个数适当排序后，即可成为等差数列，也可成为等比数列，则a+b的值为（ ）
    A.7
    B.8
    C.9
    D.10

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】假设每天从甲地去乙地的旅客人数X是服从正态分布N(800,502)的随机变量,若一天中从甲地去乙地的旅客人数不超过900的概率为p0,则p0的值为 ( )

    A. 0.954 4 B. 0.682 6 C. 0.997 4 D. 0.977 2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如图所示的频率分布直方图.

    (1)求这500件产品质量指标值的样本平均数和样本方差s2(同一组中的数据用该组区间的中点值作代表).

    (2)由直方图可以认为,这种产品的质量指标值Z服从正态分布N(μ,σ2),其中μ近似为样本平均数,σ2近似为样本方差s2.

    ①利用该正态分布,求P(187.8<Z<212.2);

    ②某用户从该企业购买了100件这种产品,记X表示这100件产品中质量指标值位于区间(187.8,212.2)上的产品件数,利用①的结果,求E(X).

    附:≈12.2.

    若Z~N(μ,σ2),则P(μ-σ<Z<μ+σ)=0.682 6,P(μ-2σ<Z<μ+2σ)=0.954 4.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）=lnx﹣ ax2﹣2x，其中a≤0．
    （1）若曲线y=f（x）在点（1，f（1））处的切线方程为y=2x+b，求a﹣2b的值；
    （2）讨论函数f（x）的单调性；
    （3）设函数g（x）=x2﹣3x+3，如果对于任意的x，t∈（0，1]，都有f（x）≤g（t）恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数y=f(x)的导函数y=f'(x)的图像如图所示.

    则下列说法中正确的是____(填序号).

    ①函数y=f(x)在区间上单调递增;

    ②函数y=f(x)在区间上单调递减;

    ③函数y=f(x)在区间(4,5)上单调递增;

    ④当x=2时,函数y=f(x)有极小值;

    ⑤当x=-时,函数y=f(x)有极大值.

    查看答案和解析>>

    同步练习册答案