
【题目】在平面四边形![]() 中,
中,![]() 、
、![]() 分
分![]() 、
、![]() 所成的比为
所成的比为![]() ,即
,即![]() ,则有:
,则有:![]() .
.

(1)拓展到空间,写出空间四边形![]() 类似的命题,并加以证明;
类似的命题,并加以证明;
(2)在长方体![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,利用上述(1)的结论求线段
的中点,利用上述(1)的结论求线段![]() 的长度;
的长度;
(3)在所有棱长均为![]() 平行六面体
平行六面体![]() 中,
中,![]() (
(![]() 为锐角定值),
为锐角定值),![]() 、
、![]() 分
分![]() 、
、![]() 所成的比为
所成的比为![]() ,求
,求![]() 的长度.(用
的长度.(用![]() ,
,![]() ,
,![]() 表示)
表示)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额的商品后即可参加一次抽奖.随着抽奖活动的有效开展,参与抽奖活动的人数越来越多,该商场对前5天抽奖活动的人数进行统计,y表示第x天参加抽奖活动的人数,得到统计表如下:
x | 1 | 2 | 3 | 4 | 5 |
y | 50 | 60 | 70 | 80 | 100 |
经过进一步统计分析,发现y与x具有线性相关关系.
(1)若从这5天随机抽取两天,求至少有1天参加抽奖人数超过70的概率;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ,并估计该活动持续7天,共有多少名顾客参加抽奖?
,并估计该活动持续7天,共有多少名顾客参加抽奖?
参考公式及数据: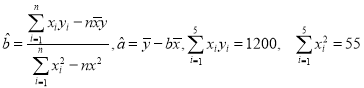 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】方程![]() 的曲线即为函数
的曲线即为函数![]() 的图像,对于函数
的图像,对于函数![]() ,有如下结论:①
,有如下结论:①![]() 在
在![]() 上单调递减;②函数
上单调递减;②函数![]() 不存在零点;③
不存在零点;③ ![]() 的最大值为
的最大值为![]() ;④若函数
;④若函数![]() 和
和![]() 的图像关于原点对称,则
的图像关于原点对称,则![]() 由方程
由方程![]() 确定;其中所有正确的命题序号是( )
确定;其中所有正确的命题序号是( )
A.③④B.②③C.①④D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对![]() 四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”; 乙说:“
作品获得一等奖”; 乙说:“ ![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“ ![]() 两件作品未获得一等奖”; 丁说:“是
两件作品未获得一等奖”; 丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
评奖揭晓后,发现这四位同学中只有两位说的话是对的,则获得一等奖的作品是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小区所有263户家庭人口数分组表示如下:
家庭人口数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
家庭数 | 20 | 29 | 48 | 50 | 46 | 36 | 19 | 8 | 4 | 3 |
(1)若将上述家庭人口数的263个数据分布记作![]() ,平均值记作
,平均值记作![]() ,写出人口数方差的计算公式(只要计算公式,不必计算结果);
,写出人口数方差的计算公式(只要计算公式,不必计算结果);
(2)写出他们家庭人口数的中位数(直接给出结果即可);
(3)计算家庭人口数的平均数与标准差.(写出公式,再利用计算器计算,精确到0.01)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,动点
,动点![]() 到直线
到直线![]() 的距离与动点
的距离与动点![]() 到点
到点![]() 的距离之比为
的距离之比为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 作任一直线交曲线
作任一直线交曲线![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 的垂线交直线
的垂线交直线![]() 于点
于点![]() ,求证:
,求证:![]() 平分线段
平分线段![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 件产品中,有
件产品中,有![]() 件正品,
件正品,![]() 件次品,从这
件次品,从这![]() 件产品中任意抽取
件产品中任意抽取![]() 件.
件.
(1)共有多少种不同的抽法?
(2)抽出的![]() 件中恰有
件中恰有![]() 件次品的抽法有多少种?
件次品的抽法有多少种?
(3)抽出的![]() 件中至少有
件中至少有![]() 件次品的抽法有多少种?
件次品的抽法有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在下列命题中,
①从分别标有1,2,……,9的9张卡片中不放回地随机抽取2次,每次抽取1张,则抽到的2张卡片上的数奇偶性不同的概率是![]() ;
;
②![]() 的展开式中的常数项为2;
的展开式中的常数项为2;
③设随机变量![]() ,若
,若![]() ,则
,则![]() .
.
其中所有正确命题的序号是( )
A.②B.①③
C.②③D.①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com