
【题目】已知圆![]() 的圆心在直线
的圆心在直线![]() :
:![]() 上,圆
上,圆![]() 被
被![]() 轴截得弦长为4,且过点
轴截得弦长为4,且过点![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)若点![]() 为直线
为直线![]() :
:![]() 上的动点,由点
上的动点,由点![]() 向圆
向圆![]() 作切线,求切线长的最小值.
作切线,求切线长的最小值.
科目:高中数学 来源: 题型:
【题目】已知直线l的方程为y=![]() x-2
x-2![]() ,又直线l过椭圆C:
,又直线l过椭圆C:![]() (a>b>0)的右焦点,且椭圆的离心率为
(a>b>0)的右焦点,且椭圆的离心率为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点D(0,1)的直线与椭圆C交于点A,B,求△AOB的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,O、E分别是BD、BC的中点,![]() ,
,![]() .
.
(1)求证:![]() 平面BCD;
平面BCD;
(2)求异面直线AB与CD所成角的余弦值;
(3)求点E到平面ACD的距离。

查看答案和解析>>
科目:高中数学 来源: 题型:
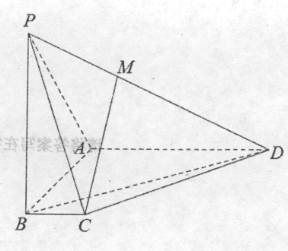
【题目】如图,在四棱锥![]() 中:
中:![]() 底面ABCD,底面ABCD为梯形,
底面ABCD,底面ABCD为梯形,![]() ,
,![]() ,且
,且![]() ,BC=1,M为棱PD上的点。
,BC=1,M为棱PD上的点。
(Ⅰ)若![]() ,求证:
,求证:![]() 平面PAB;
平面PAB;
(Ⅱ)求直线BD与平面PAD所成角的大小;
(Ⅲ)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为增强市民的环境保护意识,某市面向全市学校征召100名教师做义务宣传志愿者,成立环境保护宣传组,现把该组的成员按年龄分成5组,如下表所示:
组别 | 年龄 | 人数 |
1 |
| 5 |
2 |
| 35 |
3 |
| 20 |
4 |
| 30 |
5 |
| 10 |
(Ⅰ)若从第3,4,5组中用分层抽样的方法选出6名志愿者参加某社区宣传活动,应从第3,4,5组各选出多少名志愿者?
(Ⅱ)在Ⅰ的条件下,宣传组决定在这6名志愿者中随机选2名志愿者介绍宣传经验.
(ⅰ)列出所有可能结果;
(ⅱ)求第4组至少有1名志愿者被选中的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“割圆术”是刘徽最突出的数学成就之一,他在《九章算术注》中提出割圆术,并作为计算圆的周长,面积已经圆周率的基础,刘徽把圆内接正多边形的面积一直算到了正3072边形,并由此而求得了圆周率为3.1415和3.1416这两个近似数值,这个结果是当时世界上圆周率计算的最精确数据.如图,当分割到圆内接正六边形时,某同学利用计算机随机模拟法向圆内随机投掷点,计算得出该点落在正六边形内的频率为0.8269,那么通过该实验计算出来的圆周率近似值为(参考数据:![]() )
)

A. 3.1419B. 3.1417C. 3.1415D. 3.1413
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信运动”已经成为当下最热门的健身方式,小李的微信朋友圈内也有大量的好友参加了“微信运动”.他随机的选取了其中30人,记录了他们某一天走路的步数,将数据整理如下:
步数 |
|
|
|
人数 | 5 | 13 | 12 |
(1)若采用样本估计总体的方式,试估计小李所有微信好友中每日走路步数超过5000步的概率;
(2)已知某人一天的走路步数若超过8000步则他被系统评定为“积极型”,否则评定为“懈怠型”,将这30人按照“积极型”、“懈怠型”分成两层,进行分层抽样,从中抽取5人,将这5人中属于“积极型”的人依次记为![]() ,属于“懈怠型”的人依次记为
,属于“懈怠型”的人依次记为![]() ,现再从这5人中随机抽取2人接受问卷调查.设
,现再从这5人中随机抽取2人接受问卷调查.设![]() 为事件“抽取的2人来自不同的类型”,求事件
为事件“抽取的2人来自不同的类型”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲、乙、丙、丁、戊五名志愿者中选派三人分别从事翻译、导游、礼仪三项不同工作,若其中乙和丙只能从事前两项工作,其余三人均能从事这三项工作,则不同的选派方案共有( )
A.36种B.12种C.18种D.24种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com