练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在正方体中，是棱的中点，是侧面内的动点,且与平面的垂线垂直，如图所示，下列说法不正确的序号为__________

    ①点的轨迹是一条线段.②与是异面直线.

    ③与不可能平行.④三棱锥的体积为定值.

    【答案】③

    【解析】

    分别根据线面平行的性质定理以及异面直线的定义，以及体积公式分别进行判断.

    对于①，设平面与直线交于点，连接，则为的中点..

    分别取的中点，连接，

    则平面，平面.

    所以平面，同理可得平面

    是平面内的相交直线.

    所以平面平面，

    由与平面的垂线垂直,则平面，可得直线平面.

    即点是线段上的动点，所以①正确.

    对于②，由①有点在线段上，所以三点在侧面内.

    假设与不是异面直线，则四点共面,则他们共面于侧面内.

    这与在正方体中，显然产生矛盾，所以假设不成立.

    故与是异面直线，故②正确.

    对于③，当与重合时，，所以③错误.

    对于④，,,则平面.

    则点到平面的距离等于点(或点)到平面的距离.

    设点(或点)到平面的距离为.

    则，即.

    在正方体中，，，均为定值，所以为定值.

    点到平面的距离为定值，又为定值.

    所以的体积为定值,故④正确.

    故答案为：③.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】有一块半圆形的空地，直径米，政府计划在空地上建一个形状为等腰梯形的花圃，如图所示，其中为圆心，，在半圆上，其余为绿化部分，设.

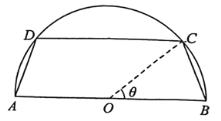
    （1）记花圃的面积为，求的最大值；

    （2）若花圃的造价为10元/米，在花圃的边、处铺设具有美化效果的灌溉管道，铺设费用为500元/米，两腰、不铺设，求满足什么条件时，会使总造价最大.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在平面直角坐标系，将曲线上的每一个点的横坐标保持不变，纵坐标缩短为原来的，得到曲线，以坐标原点为极点， 轴的正半轴为极轴，建立极坐标系， 的极坐标方程为．

    （Ⅰ）求曲线的参数方程；

    （Ⅱ）过原点且关于轴对称的两条直线与分别交曲线于、和、，且点在第一象限，当四边形的周长最大时，求直线的普通方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】四色猜想是世界三大数学猜想之一，1976年数学家阿佩尔与哈肯证明，称为四色定理.其内容是：“任意一张平面地图只用四种颜色就能使具有共同边界的国家涂上不同的颜色.”用数学语言表示为“将平面任意地细分为不相重叠的区域，每一个区域总可以用，，，四个数字之一标记，而不会使相邻的两个区域得到相同的数字.”如图，网格纸上小正方形的边长为，粗实线围城的各区域上分别标有数字，，，的四色地图符合四色定理，区域和区域标记的数字丢失.若在该四色地图上随机取一点，则恰好取在标记为的区域的概率所有可能值中，最大的是（ ）

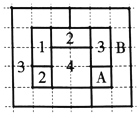
    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】[2019·潍坊期末]某钢铁加工厂新生产一批钢管，为了了解这批产品的质量状况，检验员随机抽取了100件钢管作为样本进行检测，将它们的内径尺寸作为质量指标值，由检测结果得如下频率分布表和频率分布直方图：

    分组

    频数

    频率

    25.05～25.15

    2

    0.02

    25.15～25.25

    25.25～25.35

    18

    25.35～25.45

    25.45～25.55

    25.55～25.65

    10

    0.1

    25.65～25.75

    3

    0.03

    合计

    100

    1

    （1）求，；

    （2）根据质量标准规定：钢管内径尺寸大于等于25.75或小于25.15为不合格，钢管尺寸在或为合格等级，钢管尺寸在为优秀等级，钢管的检测费用为0.5元/根．

    （i）若从和的5件样品中随机抽取2根，求至少有一根钢管为合格的概率；

    （ii）若这批钢管共有2000根，把样本的频率作为这批钢管的频率，有两种销售方案：

    ①对该批剩余钢管不再进行检测，所有钢管均以45元/根售出；

    ②对该批剩余钢管一一进行检测，不合格产品不销售，合格等级的钢管50元/根，优等钢管60元/根．

    请你为该企业选择最好的销售方案，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，正方形所在平面与等腰梯形所在平面互相垂直，已知，，.

    （1）求证：平面平面；

    （2）求平面与平面所成锐二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】建设生态文明，是关系人民福祉，关乎民族未来的长远大计.某市通宵营业的大型商场，为响应节能减排的号召，在气温超过时，才开放中央空调降温，否则关闭中央空调.如图是该市夏季一天的气温（单位：）随时间（，单位：小时）的大致变化曲线，若该曲线近似的满足函数关系.

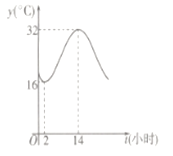
    （1）求函数的表达式；

    （2）请根据（1）的结论，判断该商场的中央空调应在本天内何时开启？何时关闭？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某种新产品投放市场一段时间后，经过调研获得了时间（天数）与销售单价（元）的一组数据，且做了一定的数据处理（如表），并作出了散点图（如图）

    表中，.

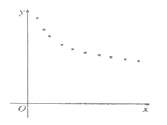
    （1）根据散点图判断，与哪一个更适宜作价格关于时间的回归方程类型？（不必说明理由）

    （2）根据判断结果和表中数据，建立关于的回归方程；

    （3）若该产品的日销售量（件）与时间的函数关系为（），求该产品投放市场第几天的销售额最高？最高为多少元？（结果保留整数）

    附：对于一组数据，，，，，其回归直线的斜率和截距的最小二乘估计分别为，.

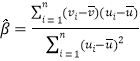    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】瑞士著名数学家欧拉在1765年提出定理：三角形的外心、重心、垂心位于同一直线上.这条直线被后人称为三角形的“欧拉线”.在平面直角坐标系中作△ABC，AB＝AC＝4，点B(－1，3)，点C(4，－2)，且其“欧拉线”与圆M：相切，则下列结论正确的是（ ）

    A.圆M上点到直线的最小距离为2

    B.圆M上点到直线的最大距离为3

    C.若点（x，y）在圆M上，则的最小值是

    D.圆与圆M有公共点，则a的取值范围是

    查看答案和解析>>

    同步练习册答案