
分析 (Ⅰ)结合二次函数的图象和函数图象的纵向对折变换,可得函数f(x)的图象;
(Ⅱ)令f(x)=5,求出方程的根,进而结合(Ⅰ)中图象可得集合A,由集合包含关系的定义,可得A,B之间的关系.
解答 解:(Ⅰ)函数f(x)=|x2-4x-5|的图象如下图所示: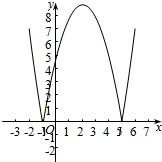
(Ⅱ)B?A理由如下:
令f(x)=5,则x2-4x-5=5或x2-4x-5=-5,
解得:x=2-$\sqrt{14}$,或x=2+$\sqrt{14}$,或x=0,或x=4,
结合(Ⅰ)中图象可得集合A={x|f(x)≥5}=(-∞,2-$\sqrt{14}$]∪[0,4]∪[2+$\sqrt{14}$,+∞).
∵2-$\sqrt{14}$>-2,2+$\sqrt{14}$<6,
故B?A.
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | 0 | C. | 6 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com