
【题目】某人将编号分别为1,2,3,4,5的5个小球随机放入编号分别为1,2,3,4,5的5个盒子中,每个盒子中放一个小球若球的编号与盒子的编号相同,则视为“放对”,否则视为“放错”,则全部“放错”的情况有________种.
【答案】44
【解析】
可以利用计数原理从正面求解问题,先算出所有情况的种数,然后分别计算有1,2,3,4,5个小球“放对”的情况,最后相减即可得到结果.
解法一 第一步,若1号盒子“放错”,则1号盒子有![]() 种不同的情况;
种不同的情况;
第二步,考虑与1号盒子中所放小球的编号相同的盒子中的情况,
若该盒子中的小球编号恰好为1,则5个小球全部“放错”的情况有![]() (种),
(种),
若该盒子中的小球编号不是1,则5个小球全部“放错”的情况有![]() (种).
(种).
由计数原理可知,5个小球全部“放错”的情况有![]() (种).
(种).
解法二 将5个小球放入5个盒子中,共有![]() 种不同的放法,
种不同的放法,
其中恰有1个小球“放对”的情况有![]() (种),
(种),
恰有2个小球“放对”的情况有![]() (种),
(种),
恰有3个小球“放对”的情况有![]() (种),
(种),
恰有4个小球“放对”的情况有0种,
恰有5个小球“放对”的情况有1种,
故全部“放错”的情况有![]() (种).
(种).
故答案为:44


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为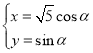 (其中
(其中![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() 、
、![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() :
:![]() 与曲线
与曲线![]() ,
,![]() 分别交于点
分别交于点![]() ,
,![]() (且点
(且点![]() ,
,![]() 均异于原点
均异于原点![]() ),当
),当![]() 时,求
时,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱柱![]() 中,侧面
中,侧面![]() 为菱形,
为菱形,![]() ,
,![]() ,侧面
,侧面![]() 为正方形,平面
为正方形,平面![]() 平面
平面![]() .点
.点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
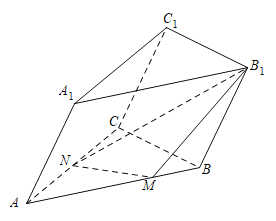
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年的3月12日是植树节,某公司为了动员职工积极参加植树造林,在植树节期间开展植树有奖活动,设有甲、乙两个摸奖箱,每位植树者植树每满30棵获得一次甲箱内摸奖机会,植树每满50棵获得一次乙箱内摸奖机会,每箱内各有10个球(这些球除颜色外全相同),甲箱内有红、黄、黑三种颜色的球,其中![]() 个红球,
个红球,![]() 个黄球,5个黑球,乙箱内有4个红球和6个黄球,每次摸一个球后放回原箱,摸得红球奖100元,黄球奖50元,摸得黑球则没有奖金.
个黄球,5个黑球,乙箱内有4个红球和6个黄球,每次摸一个球后放回原箱,摸得红球奖100元,黄球奖50元,摸得黑球则没有奖金.
(1)经统计,每人的植树棵数![]() 服从正态分布
服从正态分布![]() ,若其中有200位植树者参与了抽奖,请估计植树的棵数
,若其中有200位植树者参与了抽奖,请估计植树的棵数![]() 在区间
在区间![]() 内并中奖的人数(结果四舍五入取整数);
内并中奖的人数(结果四舍五入取整数);
附:若![]() ,则
,则![]() ,
,
![]() .
.
(2)若![]() ,某位植树者获得两次甲箱内摸奖机会,求中奖金额
,某位植树者获得两次甲箱内摸奖机会,求中奖金额![]() (单位:元)的分布列;
(单位:元)的分布列;
(3)某人植树100棵,有两种摸奖方法,
方法一:三次甲箱内摸奖机会;
方法二:两次乙箱内摸奖机会;
请问:这位植树者选哪一种方法所得奖金的期望值较大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,过点![]() 的直线l与抛物线
的直线l与抛物线![]() 交于A,B两点,以AB为直径作圆,记为
交于A,B两点,以AB为直径作圆,记为![]() ,
,![]() 与抛物线C的准线始终相切.
与抛物线C的准线始终相切.
(1)求抛物线C的方程;
(2)过圆心M作x轴垂线与抛物线相交于点N,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司准备设计一个精美的心形巧克力盒子,它是由半圆![]() 、半圆
、半圆![]() 和正方形ABCD组成的,且
和正方形ABCD组成的,且![]() .设计人员想在心形盒子表面上设计一个矩形的标签EFGH,标签的其中两个顶点E,F在AM上,另外两个顶点G,H在CN上(M,N分别是AB,CB的中点).设EF的中点为P,
.设计人员想在心形盒子表面上设计一个矩形的标签EFGH,标签的其中两个顶点E,F在AM上,另外两个顶点G,H在CN上(M,N分别是AB,CB的中点).设EF的中点为P,![]() ,矩形EFGH的面积为
,矩形EFGH的面积为![]() .
.
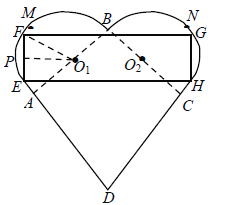
(1)写出S关于![]() 的函数关系式
的函数关系式![]()
(2)当![]() 为何值时矩形EFGH的面积最大?
为何值时矩形EFGH的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在定义域上单调增,求
在定义域上单调增,求![]() 的取值范围;
的取值范围;
(3)若函数![]() 在定义域上不单调,试判定
在定义域上不单调,试判定![]() 的零点个数,并给出证明过程.
的零点个数,并给出证明过程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,斜三棱柱![]() 中,
中,![]() 是边长为2的正三角形,
是边长为2的正三角形,![]() 为
为![]() 的中点,
的中点,![]() 平面
平面![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,
,![]() 为
为![]() 与
与![]() 的交点,且
的交点,且![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.
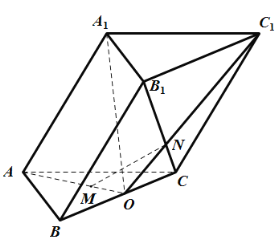
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校拟从甲、乙两名同学中选一人参加疫情知识问答竞赛,于是抽取了甲、乙两人最近同时参加校内竞赛的十次成绩,将统计情况绘制成如图所示的折线图.根据该折线图,下面结论正确的是( )
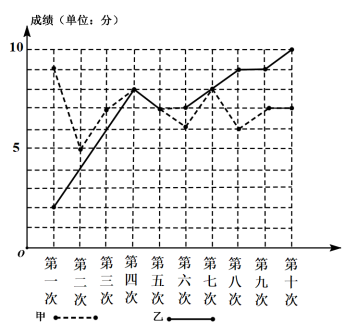
A.甲、乙成绩的中位数均为7
B.乙的成绩的平均分为6.8
C.甲从第四次到第六次成绩的下降速率要大于乙从第四次到第五次的下降速率
D.甲的成绩的方差小于乙的成绩的方差
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com