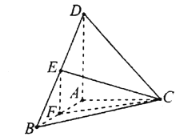
【题目】如图，三棱锥D-ABC中，
，E，F分别为DB，AB的中点，且
.
（1）求证：平面
平面ABC；
（2）求点D到平面CEF的距离.
【答案】（1）证明见解析；（2）
.
【解析】
（1）取BC的中点G，连接AG，DG，可证
平面DAG，可得
，再由
，
，可证
，可得
平面ABC，即可证明结论；
（2）由条件可得点D到平面CEF的距离等于点B到平面CEF的距离，求出三棱锥
的体积和
的面积，用等体积法，即可求解.
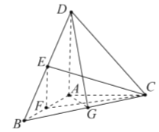
（1）如图，取BC的中点G，连接AG，DG，
因为
，所以
，
因为
，所以
，
又因为
，
所以平面DAG，所以.
因为E，F分别为DB，AB的中点，所以.
因为，即
，则.
又因为
，所以平面ABC，
又因为
平面DAB，所以平面
平面ABC.
（2）因为点E为DB的中点，
所以点D到平面CEF的距离等于点B到平面CEF的距离.
设点D到平面CEF的距离为h，
因为
，又因为
平面ABC，
所以
，
在
中，
.
所以
，
在
中，
，
所以
，
又因为
，
所以
，
而
，
则
.
所以点D到平面CEF的距离为.
科目：高中数学 来源： 题型：
【题目】如下图中
、
、
、
、
、
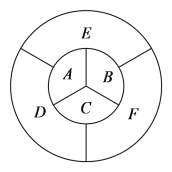
六个区域进行染色，每个区域只染一种颜色，每个区域只染一种颜色，且相邻的区域不同色.若有
种颜色可供选择，则共有_________种不同的染色方案.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知某保险公司的某险种的基本保费为
（单位：元），继续购买该险种的投保人称为续保人，续保人本年度的保费与其上年度出险次数的关联如下：
上年度出险次数 | 0 | 1 | 2 | 3 |
|
保费（元） |
|
|
|
|
|
随机调查了该险种的400名续保人在一年内的出险情况，得到下表：
出险次数 | 0 | 1 | 2 | 3 |
|
频数 | 280 | 80 | 24 | 12 | 4 |
该保险公司这种保险的赔付规定如下：
出险序次 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次及以上 |
赔付金额（元） |
|
|
|
| 0 |
将所抽样本的频率视为概率.
（Ⅰ）求本年度续保人保费的平均值的估计值；
（Ⅱ）按保险合同规定，若续保人在本年度内出险3次，则可获得赔付
元；若续保人在本年度内出险6次，则可获得赔付
元；依此类推，求本年度续保人所获赔付金额的平均值的估计值；
（Ⅲ）续保人原定约了保险公司的销售人员在上午10:30~11:30之间上门签合同，因为续保人临时有事，外出的时间在上午10:45~11:05之间，请问续保人在离开前见到销售人员的概率是多少？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系
中，曲线
的参数方程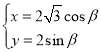
（
为参数）.直线
的参数方程
（
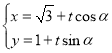为参数）.
（Ⅰ）求曲线在直角坐标系中的普通方程；
（Ⅱ）以坐标原点
为极点，
轴的正半轴为极轴建立极坐标系，当曲线截直线所得线段的中点极坐标为
时，求直线的倾斜角.
查看答案和解析>>
科目：高中数学 来源： 题型：
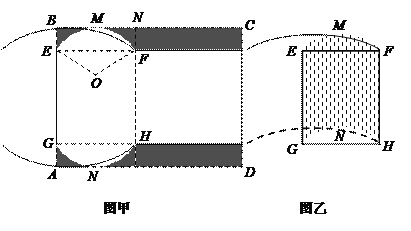
【题目】有一矩形硬纸板材料（厚度忽略不计），一边
长为6分米，另一边足够长．现从中截取矩形
（如图甲所示），再剪去图中阴影部分，用剩下的部分恰好能折卷成一个底面是弓形的柱体包装盒（如图乙所示，重叠部分忽略不计），其中
是以
为圆心、
的扇形，且弧
,
分别与边
, 
相切于点
, 
．
（1）当
长为1分米时，求折卷成的包装盒的容积；
（2）当
的长是多少分米时，折卷成的包装盒的容积最大？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列四个命题：①任意两条直线都可以确定一个平面；②若两个平面有3个不同的公共点，则这两个平面重合；③直线a，b，c，若a与b共面，b与c共面，则a与c共面；④若直线l上有一点在平面α外，则l在平面α外.其中错误命题的个数是（ ）
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
