
| C | 2 n |
| C | 3 n |
| C | 4 n |
| C | 2 n |
| C | 3 n |
| C | 4 n |
| (n+1)n(n-1) |
| 3×2×1 |
| n×(n-1)×(n-2)×(n-3) |
| 4×3×2×1 |
| C | 2 n |
| C | 3 n |
| C | 4 n |
| (n+1)n(n-1) |
| 3×2×1 |
| n×(n-1)×(n-2)×(n-3) |
| 4×3×2×1 |
9+
| ||
| 2 |
9-
| ||
| 2 |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:贵州省毕节市第一中学2012届高三第四次摸底考试数学试题 题型:013
(理)已知n是正整数,实数a是常数,若![]() (
(![]() +
+![]() +
+![]() +…+
+…+![]() )=9,则a的值是
)=9,则a的值是
![]()
![]()
![]() 和
和![]()
-![]() 和-
和-![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
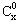 =1,这是组合数
=1,这是组合数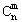 (n、m是正整数,且m≤n)的一种推广.
(n、m是正整数,且m≤n)的一种推广.
(1)求C![]() 的值;
的值;
(2)组合数的两个性质;
①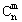 =C
=C![]() . ②
. ②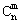 +C
+C![]() =C
=C![]() .
.
是否都能推广到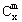 (x∈R,m是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.
(x∈R,m是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.
(3)已知组知数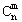 是正整数,证明:当x∈Z,m是正整数时,
是正整数,证明:当x∈Z,m是正整数时,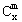 ∈Z
∈Z
查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京市西城区(北区)高二(下)期末数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com