
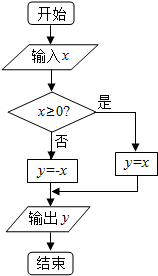
 阅读如图所示的程序框图.
阅读如图所示的程序框图.分析 (1)由已知中的程序框图,分析两条分支上的语句,可得函数的解析式;
(2)求出数y=f(x)表示的曲线与直线y=1围成的三角形面积,及其内切圆的面积,代入由几何概型概率计算公式,可得答案.
解答 解:(1)由已知中的程序框图可得:
函数y=f(x)=$\left\{\begin{array}{l}-x,x<0\\ x,x≥0\end{array}\right.$,
(2)如图所示: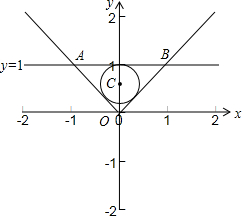
当y=1时,A点坐标为(-1,1),B点坐标为:(1,1),
故OA=OB=$\sqrt{2}$,AB=2,
则△OAB的面积S=$\frac{1}{2}×\sqrt{2}×\sqrt{2}$=1,
△OAB的内切圆半径r=$\frac{\sqrt{2}+\sqrt{2}-2}{2}$=$\sqrt{2}-1$,
故圆C的面积为:$π(\sqrt{2}-1)^{2}$=(3-2$\sqrt{2}$)π,
故向这个三角形内随机投掷一粒黄豆,求这粒黄豆落入圆C的概率P=(3-2$\sqrt{2}$)π.
点评 本题考查的知识点是分段函数,程序框图和几何概率,是算法,函数和概率的综合应用,难度中档.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,2) | B. | [$\frac{3}{2}$,2) | C. | (-∞,2] | D. | (-∞,$\frac{3}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 0 | C. | 1 | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽豪州蒙城县一中高二上月考一数学试卷(解析版) 题型:解答题
设数列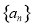 的前
的前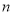 项和为
项和为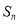 ,
,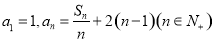 .
.
(1)证明:数列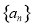 为等差数列,并分别求出
为等差数列,并分别求出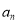 和
和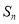 ;
;
(2)设数列 的前
的前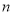 项和为
项和为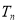 ,证明:
,证明: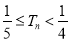 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com