
【题目】已知函数![]() ,其中
,其中![]() ,
,![]() .
.
(1)函数![]() 的图象能否与x轴相切?若能,求出实数a;若不能,请说明理由.
的图象能否与x轴相切?若能,求出实数a;若不能,请说明理由.
(2)若![]() 在
在![]() 处取得极大值,求实数a的取值范围.
处取得极大值,求实数a的取值范围.
【答案】(1) 答案见解析(2) ![]()
【解析】
(1)假设函数![]() 的图象与x轴相切于
的图象与x轴相切于![]() ,根据相切可得方程组
,根据相切可得方程组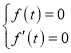 ,看方程是否有解即可;(2)求出
,看方程是否有解即可;(2)求出![]() 的导数,设
的导数,设![]() (
(![]() ),根据函数的单调性及
),根据函数的单调性及![]() 在
在![]() 处取得极大值求出a的范围即可.
处取得极大值求出a的范围即可.
(1)函数![]() 的图象不能与x轴相切,理由若下:
的图象不能与x轴相切,理由若下:
![]() .假设函数
.假设函数![]() 的图象与x轴相切于
的图象与x轴相切于![]()
则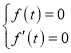 即
即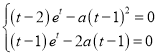
显然![]() ,
,![]() ,代入
,代入![]() 中得,
中得,![]() 无实数解.
无实数解.
故函数![]() 的图象不能与x轴相切.
的图象不能与x轴相切.
(2)![]() (
(![]() )
)
![]() ,
,![]() ,
,
设![]() (
(![]() ),
),
![]() 恒大于零.
恒大于零.
![]() 在
在![]() 上单调递增.
上单调递增.
又![]() ,
,![]() ,
,![]() ,
,![]()
∴存在唯一![]() ,使
,使![]() ,且
,且
![]() 时
时![]() ,
,![]() 时
时![]() ,
,
①当![]() 时,
时,![]() 恒成立,
恒成立,![]() 在
在![]() 单调递增,
单调递增,
![]() 无极值,不合题意.
无极值,不合题意.
②当![]() 时,可得当
时,可得当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
所以![]() 在
在![]() 内单调递减,在
内单调递减,在![]() 内单调递增,
内单调递增,
所以![]() 在
在![]() 处取得极小值,不合题意.
处取得极小值,不合题意.
③当![]() 时,可得当
时,可得当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
所以![]() 在
在![]() 内单调递增,在
内单调递增,在![]() 内单调递减,
内单调递减,
所以![]() 在
在![]() 处取得极大值,符合题意.
处取得极大值,符合题意.
此时由![]() 得
得![]() 即
即![]() ,
,
![]()
综上可知,实数a的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】“总把新桃换旧符”(王安石)、“灯前小草写桃符”(陆游),春节是中华民族的传统节日,在宋代人们用写“桃符”的方式来祈福避祸,而现代人们通过贴“福”字、贴春联、挂灯笼等方式来表达对新年的美好祝愿,某商家在春节前开展商品促销活动,顾客凡购物金额满50元,则可以从“福”字、春联和灯笼这三类礼品中任意免费领取一件,若有4名顾客都领取一件礼品,则他们中有且仅有2人领取的礼品种类相同的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,点A是直线
,点A是直线![]() 上的动点,过
上的动点,过![]() 作直线
作直线![]() ,
,![]() ,线段
,线段![]() 的垂直平分线与
的垂直平分线与![]() 交于点
交于点![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若点![]() ,
,![]() 是直线
是直线![]() 上两个不同的点,且
上两个不同的点,且![]() 的内切圆方程为
的内切圆方程为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016里约奥运会期间,小赵常看的4个电视频道中有2个频道在转播奥运比赛,若小赵这时打开电视,随机打开其中两个频道试看,那么,小赵所看到的第一个电视台恰好没有转播奥运比赛,而第二个电视台恰好在转播奥运比赛的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(k+![]() )lnx+
)lnx+![]() ,k∈[4,+∞),曲线y=f(x)上总存在两点M(x1,y1),N(x2,y2),使曲线y=f(x)在M,N两点处的切线互相平行,则x1+x2的取值范围为
,k∈[4,+∞),曲线y=f(x)上总存在两点M(x1,y1),N(x2,y2),使曲线y=f(x)在M,N两点处的切线互相平行,则x1+x2的取值范围为
A. (![]() ,+∞) B. (
,+∞) B. (![]() ,+∞) C. [
,+∞) C. [![]() ,+∞) D. [
,+∞) D. [![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 5 |
| 0 |
(1)请将上表数据补充完整,填写在答题卡上相应位置,并直接写出函数![]() 的解析式;
的解析式;
(2)将![]() 图象上所有点向左平行移动
图象上所有点向左平行移动![]() 个单位长度,并把图象上所有点的横坐标缩短为原来的
个单位长度,并把图象上所有点的横坐标缩短为原来的![]() (纵坐标不变),得到
(纵坐标不变),得到![]() 的图象.若
的图象.若![]() 图象的一个对称中心为
图象的一个对称中心为![]() ,求
,求![]() 的最小值;
的最小值;
(3)在(2)条件下,求![]() 在
在![]() 上的增区间.
上的增区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com