
设f(x)为周期是2的奇函数,当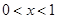 时,f(x)=x(x+1),则当
时,f(x)=x(x+1),则当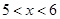 时,f(x)的表达式为
时,f(x)的表达式为
| A.(x-5)(x-4) | B.(x-6)(x-5) | C.(x-6)(5-x) | D.(x-6)(7-x) |
D
解析试题分析:利用函数是奇函数,可由x∈(0,1)时的解析式求x∈(-1,0)时的解析式,利用周期性求得x∈(5,6)时,f(x)表达式.
解:因为x∈(0,1)时,f(x)=x(x+1),
设x∈(-1,0)时,-x∈(0,1),
∴f(-x)=-x(-x+1),
∵f(x)为定义在R上的奇函数
∴f(x)=-f(-x)=x(-x+1),
∴当x∈(-1,0)时,f(x)=x(-x+1),
所以x∈(5,6)时,x-6∈(-1,0),
∵f(x)为周期是2的函数,
∴f(x)=f(x-6)=(x-6)(6-x+1)=(x-6)(7-x),
故选D
考点:抽象函数的运用
点评:本题综合考查函数奇偶性与周期性知识的运用,把要求区间上的问题转化到已知区间上求解,是解题的关键,体现了转化的数学思想方法.属中档题


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中数学 来源: 题型:单选题
设 是( )
是( )
| A.奇函数,在(0,+∞)上是减函数 | B.偶函数,在(0,+∞)上是减函数 |
| C.奇函数,在(0,+∞)上是增函数 | D.偶函数,在(0,+∞)上是增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
下面有四个结论:①偶函数的图像一定与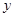 轴相交。②奇函数的图像不一定过原点。③偶函数若在
轴相交。②奇函数的图像不一定过原点。③偶函数若在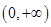 上是减函数,则在
上是减函数,则在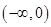 上一定是增函数。④有且只有一个函数既是奇函数又是偶函数。其中正确结论的个数是( )
上一定是增函数。④有且只有一个函数既是奇函数又是偶函数。其中正确结论的个数是( )
| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com