
【题目】如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AD//BC,BC=2AD,AD⊥CD,PD⊥平面ABCD,E为PB的中点.
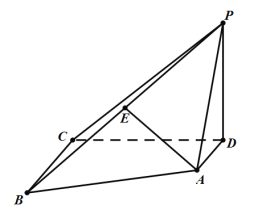
(1)求证:AE//平面PDC;
(2)若BC=CD=PD,求直线AC与平面PBC所成角的余弦值.
科目:高中数学 来源: 题型:
【题目】某学校为了选拔学生参加“XX市中学生知识竞赛”,先在本校进行选拔测试,若该校有100名学生参加选拔测试,并根据选拔测试成绩作出如图所示的频率分布直方图.
(1)根据频率分布直方图,估算这100名学生参加选拔测试的平均成绩;
(2)该校推荐选拔测试成绩在110以上的学生代表学校参加市知识竞赛,为了了解情况,在该校推荐参加市知识竞赛的学生中随机抽取2人,求选取的两人的选拔成绩在频率分布直方图中处于不同组的概率.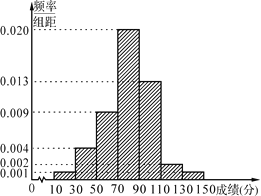
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】互联网![]() 时代的今天,移动互联快速发展,智能手机
时代的今天,移动互联快速发展,智能手机![]() 技术不断成熟,价格却不断下降,成为了生活中必不可少的工具
技术不断成熟,价格却不断下降,成为了生活中必不可少的工具![]() 中学生是对新事物和新潮流反应最快的一个群体之一
中学生是对新事物和新潮流反应最快的一个群体之一![]() 逐渐地,越来越多的中学生开始在学校里使用手机
逐渐地,越来越多的中学生开始在学校里使用手机![]() 手机特别是智能手机在让我们的生活更便捷的同时会带来些问题,同学们为了解手机在中学生中的使用情况,对本校高二年级100名同学使用手机的情况进行调查
手机特别是智能手机在让我们的生活更便捷的同时会带来些问题,同学们为了解手机在中学生中的使用情况,对本校高二年级100名同学使用手机的情况进行调查![]() 针对调查中获得的“每天平均使用手机进行娱乐活动的时间”进行分组整理得到如图4的饼图、
针对调查中获得的“每天平均使用手机进行娱乐活动的时间”进行分组整理得到如图4的饼图、![]() 注:图中
注:图中![]() 2,
2,![]() 单位:小时
单位:小时![]() 代表分组为
代表分组为![]() i的情况
i的情况![]()

![]() 求饼图中a的值;
求饼图中a的值;
![]() 假设同一组中的每个数据可用给定区间的中点值代替,试估计样本中的100名学生每天平均使用手机的平均时间在第几组?
假设同一组中的每个数据可用给定区间的中点值代替,试估计样本中的100名学生每天平均使用手机的平均时间在第几组?![]() 只需写出结论
只需写出结论![]()
![]() 从该校随机选取一名同学,能否根据题目中所给信息估计出这名学生每天平均使用手机进行娱乐活动小于
从该校随机选取一名同学,能否根据题目中所给信息估计出这名学生每天平均使用手机进行娱乐活动小于![]() 小时的概率,若能,请算出这个概率;若不能,请说明理由
小时的概率,若能,请算出这个概率;若不能,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若各项为正实数的数列![]() 满足
满足![]() ,则称数列
,则称数列![]() 为“算术平方根递推数列”.
为“算术平方根递推数列”.
已知数列![]() 满足
满足![]() 且
且![]() 点
点![]() 在二次函数
在二次函数![]() 的图象上.
的图象上.
(1)试判断数列![]()
![]() 是否为算术平方根递推数列?若是,请说明你的理由;
是否为算术平方根递推数列?若是,请说明你的理由;
(2)记![]()
![]() ,求证:数列
,求证:数列![]() 是等比数列,并求出通项公式
是等比数列,并求出通项公式![]() ;
;
(3)从数列![]() 中依据某种顺序自左至右取出其中的项
中依据某种顺序自左至右取出其中的项![]() ,把这些项重新组成一个新数列
,把这些项重新组成一个新数列![]() :
:![]() .若数列
.若数列![]() 是首项为
是首项为![]() 、公比为
、公比为![]() 的无穷等比数列,且数列
的无穷等比数列,且数列![]() 各项的和为
各项的和为![]() ,求正整数
,求正整数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项都是正数的数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足
满足![]() ,求和
,求和![]() ;
;
(3)是否存在正整数![]() ,
,![]() ,
,![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等差数列?若存在,求出所有满足要求的
成等差数列?若存在,求出所有满足要求的![]() ,
,![]() ,
,![]() ,若不存在,说明理由.
,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,射线![]() 和
和![]() 均为笔直的公路,扇形
均为笔直的公路,扇形![]() 区域(含边界)是一蔬菜种植园,其中
区域(含边界)是一蔬菜种植园,其中![]() 、
、![]() 分别在射线
分别在射线![]() 和
和![]() 上.经测量得,扇形
上.经测量得,扇形![]() 的圆心角(即
的圆心角(即![]() )为
)为![]() 、半径为1千米.为了方便菜农经营,打算在扇形
、半径为1千米.为了方便菜农经营,打算在扇形![]() 区域外修建一条公路
区域外修建一条公路![]() ,分别与射线
,分别与射线![]() 、
、![]() 交于
交于![]() 、
、![]() 两点,并要求
两点,并要求![]() 与扇形弧
与扇形弧![]() 相切于点
相切于点![]() .设
.设![]() (单位:弧度),假设所有公路的宽度均忽略不计.
(单位:弧度),假设所有公路的宽度均忽略不计.
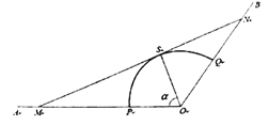
(1)试将公路![]() 的长度表示为
的长度表示为![]() 的函数,并写出
的函数,并写出![]() 的取值范围;
的取值范围;
(2)试确定![]() 的值,使得公路
的值,使得公路![]() 的长度最小,并求出其最小值.
的长度最小,并求出其最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com