
¡ŸÌâÄ¿¡¿2022Äê±±Ÿ©¶¬ŒŸ°ÂÔ˻ጎµÚ24œì¶¬ŒŸ°ÂÁÖÆ¥¿ËÔ˶¯»á£¬œ«ÔÚ2022Äê2ÔÂ4ÖÁ2ÔÂ20ÈÕÔÚ±±Ÿ©ºÍÕŌҿÚÁªºÏŸÙÐÐ.ijÑП¿»ú¹¹ÎªÁËœâŽóѧÉú¶Ô±ùºøÔ˶¯µÄÐËÈ€£¬Ëæ»úŽÓijŽóѧѧÉúÖгéÈ¡ÁË120ÈËœøÐе÷²é£¬ŸÍ³ŒÆÄÐÉúÓëÅ®ÉúµÄÈËÊýÖ®±ÈΪ11£º13£¬ÄÐÉúÖÐÓÐ30È˱íÊŸ¶Ô±ùºøÔ˶¯ÓÐÐËÈ€£¬Å®ÉúÖÐÓÐ15È˱íÊŸ¶Ô±ùºøÔ˶¯Ã»ÓÐÐËÈ€.
£š1£©Íê³É2¡Á2ÁÐÁª±í£¬²¢»ØŽðÄÜ·ñÓÐ99%µÄ°ÑÎÕÈÏΪ¡°¶Ô±ùºøÊÇ·ñÓÐÐËÈ€ÓëÐÔ±ðÓйء±£¿
ÓÐÐËÈ€ | ûÓÐÐËÈ€ | ºÏŒÆ | |
ÄÐ | 30 | ||
Å® | 15 | ||
ºÏŒÆ | 120 |
£š2£©Èôœ«ÆµÂÊÊÓΪžÅÂÊ£¬ÏÖÔÙŽÓžÃУȫÌåѧÉúÖУ¬²ÉÓÃËæ»ú³éÑùµÄ·œ·šÃ¿ŽÎ³éÈ¡1ÃûѧÉú£¬³éÈ¡5ŽÎ£¬ŒÇ±»³éÈ¡µÄ5ÃûѧÉúÖжԱùºøÓÐÐËÈ€µÄÈËÊýΪX£¬ÈôÿŽÎ³éÈ¡µÄœá¹ûÊÇÏ໥¶ÀÁ¢µÄ£¬ÇóXµÄ·Ö²ŒÁУ¬ÆÚÍûºÍ·œ²î.
žœ£º²Î¿Œ¹«Êœ![]() £¬ÆäÖÐn£œa+b+c+d.
£¬ÆäÖÐn£œa+b+c+d.
ÁÙœçÖµ±í£º
P£šK2¡ÝK0£© | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
K0 | 2.072 | 2.076 | 3.841 | 5.024 | 6.635 |
¡ŸŽð°ž¡¿£š1£©Ìî±íŒûœâÎö£»ÓÐ99%µÄ°ÑÎÕÈÏΪ¡°¶Ô±ùºøÊÇ·ñÓÐÐËÈ€ÓëÐÔ±ðÓйء±£š2£©ÏêŒûœâÎö
¡ŸœâÎö¡¿
£š1£©ÏÈžùŸÝ±ÈÀý¹ØϵÇóœâÄÐŮͬѧµÄÈËÊý£¬Íê³É±ížñ£¬Çóœâ¹Û²âÖµµÃ³öœáÂÛ£»
£š2£©žùŸÝ¶þÏî·Ö²ŒµÄÌصãÇóœâ·Ö²ŒÁкÍÆÚÍû¡¢·œ²î.
£š1£©ÒòΪÄÐÉúÓëÅ®ÉúµÄÈËÊýÖ®±ÈΪ11£º13£¬ÇÒ×ÜÈËÊýΪ120£¬ËùÒÔÄÐÉú¹²ÓÐ55ÈË£¬Å®Éú¹²ÓÐ65ÈË£»±ížñÈçÏ£º
ÓÐÐËÈ€ | ûÓÐÐËÈ€ | ºÏŒÆ | |
ÄÐ | 30 | 25 | 55 |
Å® | 50 | 15 | 65 |
ºÏŒÆ | 80 | 40 | 120 |
žùŸÝ±ížñÇó³öK2![]() £¬
£¬
¹ÊÓÐ99%µÄ°ÑÎÕÈÏΪ¡°¶Ô±ùºøÊÇ·ñÓÐÐËÈ€ÓëÐÔ±ðÓйء±.
£š2£©ÓÉÁбí¿ÉÖª£¬¶Ô±ùºøÓÐÐËÈ€µÄѧÉúƵÂÊΪ![]() £¬œ«ÆäÊÓΪžÅÂÊ£¬
£¬œ«ÆäÊÓΪžÅÂÊ£¬
ÓÉÌâÒâX¡«B£š5£¬![]() £©£¬
£©£¬
X | 0 | 1 | 2 | 3 | 4 | 5 |
P |
|
|
|
|
|
|
E£šX£©£œnp![]() £¬D£šx£©£œnpq
£¬D£šx£©£œnpq![]() .
.



| Äꌶ | žßÖÐ¿Î³Ì | Äꌶ | ³õÖÐ¿Î³Ì |
| žßÒ» | žßÒ»Ãâ·Ñ¿Î³ÌÍÆŒö£¡ | ³õÒ» | ³õÒ»Ãâ·Ñ¿Î³ÌÍÆŒö£¡ |
| žß¶þ | žß¶þÃâ·Ñ¿Î³ÌÍÆŒö£¡ | ³õ¶þ | ³õ¶þÃâ·Ñ¿Î³ÌÍÆŒö£¡ |
| žßÈý | žßÈýÃâ·Ñ¿Î³ÌÍÆŒö£¡ | ³õÈý | ³õÈýÃâ·Ñ¿Î³ÌÍÆŒö£¡ |
¿ÆÄ¿£ºžßÖÐÊýѧ ÀŽÔŽ£º ÌâÐÍ£º
¡ŸÌâÄ¿¡¿ÒÑÖªº¯Êý![]() £®
£®
£š1£©ÉèŠÈ¡Ê[0£¬ŠÐ]£¬ÇÒf£šŠÈ£©![]() 1£¬ÇóŠÈµÄÖµ£»
1£¬ÇóŠÈµÄÖµ£»
£š2£©ÔÚ¡÷ABCÖУ¬AB£œ1£¬f£šC£©![]() 1£¬ÇÒ¡÷ABCµÄÃæ»ýΪ
1£¬ÇÒ¡÷ABCµÄÃæ»ýΪ![]() £¬ÇósinA+sinBµÄÖµ£®
£¬ÇósinA+sinBµÄÖµ£®
²é¿ŽŽð°žºÍœâÎö>>
¿ÆÄ¿£ºžßÖÐÊýѧ ÀŽÔŽ£º ÌâÐÍ£º
¡ŸÌâÄ¿¡¿ÒÑÖªº¯Êýf£šx£©£œ|2x+3|+|2x©1|£®
£š1£©Çó²»µÈÊœf£šx£©¡Ü6µÄœâŒ¯£»
£š2£©Èô¹ØÓÚxµÄ²»µÈÊœf£šx£©£Œ|m©1|µÄœâŒ¯·Ç¿Õ£¬ÇóʵÊýmµÄÈ¡Öµ·¶Î§£®
²é¿ŽŽð°žºÍœâÎö>>
¿ÆÄ¿£ºžßÖÐÊýѧ ÀŽÔŽ£º ÌâÐÍ£º
¡ŸÌâÄ¿¡¿ÈçÍŒËùÊŸµÄ¶àÃæÌåÖУ¬![]() ÆœÃæ
ÆœÃæ![]() £¬
£¬![]() £¬
£¬![]() £¬ÇÒ
£¬ÇÒ![]() £¬µã
£¬µã![]() ÊÇ
ÊÇ![]() µÄÖе㣮
µÄÖе㣮

£š1£©ÇóÖ€£ºÆœÃæ![]() ÆœÃæ
ÆœÃæ![]() £»
£»
£š2£©Çó¶þÃæœÇ![]() µÄÓàÏÒÖµ£®
µÄÓàÏÒÖµ£®
²é¿ŽŽð°žºÍœâÎö>>
¿ÆÄ¿£ºžßÖÐÊýѧ ÀŽÔŽ£º ÌâÐÍ£º
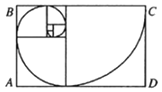
¡ŸÌâÄ¿¡¿ÈôÊýÁÐ{an}Âú×ãa1£œ1£¬a2£œ1£¬an+2£œan+an+1£¬Ôò³ÆÊýÁÐ{an}Ϊ쳲šÄÇÆõÊýÁУ¬ì³²šÄÇÆõÂÝÐýÏßÊÇžùŸÝì³²šÄÇÆõÊýÁл³öÀŽµÄÂÝÐýÇúÏߣ¬×ÔÈ»œçÖÐŽæÔÚÐí¶àì³²šÄÇÆõÂÝÐýÏßµÄÍŒ°ž£¬ÊÇ×ÔÈ»œç×îÍêÃÀµÄŸµä»Æœð±ÈÀý.×÷ÍŒ¹æÔòÊÇÔÚÒÔì³²šÄÇÆõÊýΪ±ßµÄÕý·œÐÎÆŽ³ÉµÄ³€·œÐÎÖлһžöÔ²ÐÄœÇΪ90¡ãµÄÉÈÐΣ¬Á¬ÆðÀŽµÄ»¡ÏߟÍÊÇì³²šÄÇÆõÂÝÐýÏߣ¬ÈçÍŒËùÊŸµÄ7žöÕý·œÐεı߳€·Ö±ðΪa1£¬a2£¬¡£¬a7£¬ÔÚ³€·œÐÎABCDÄÚÈÎÈ¡Ò»µã£¬ÔòžÃµã²»ÔÚÈκÎÒ»žöÉÈÐÎÄڵĞÅÂÊΪ£š £©
A.1![]() B.1
B.1![]() C.
C.![]() D.
D.![]()
²é¿ŽŽð°žºÍœâÎö>>
¿ÆÄ¿£ºžßÖÐÊýѧ ÀŽÔŽ£º ÌâÐÍ£º
¡ŸÌâÄ¿¡¿ÒÑÖªº¯Êýf(x)=![]() x
x![]() £ax+(a£1)
£ax+(a£1)![]() £¬
£¬![]() ¡£
¡£
£š1£©ÌÖÂÛº¯Êý![]() µÄµ¥µ÷ÐÔ£»
µÄµ¥µ÷ÐÔ£»
£š2£©Ö€Ã÷£ºÈô![]() £¬Ôò¶ÔÈÎÒâx
£¬Ôò¶ÔÈÎÒâx![]() £¬x
£¬x![]()
![]()
![]() £¬x
£¬x![]()
![]() x
x![]() £¬ÓÐ
£¬ÓÐ![]() ¡£
¡£
²é¿ŽŽð°žºÍœâÎö>>
¿ÆÄ¿£ºžßÖÐÊýѧ ÀŽÔŽ£º ÌâÐÍ£º
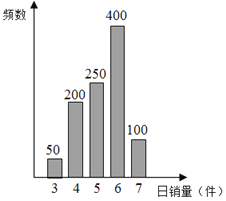
¡ŸÌâÄ¿¡¿Ä³¹«ËŸÏúÊÛ²¿Ëæ»ú³éÈ¡ÁË1000ÃûÏúÊÛÔ±1ÌìµÄÏúÊÛŒÇÂŒ£¬ŸÍ³ŒÆ£¬ÆäÖù׎͌ÈçÍŒ£®
žÃ¹«ËŸžø³öÁËÁœÖÖÈÕÐœ·œ°ž£®
·œ°ž1£ºÃ»Óе×Ðœ£¬Ã¿ÏúÊÛÒ»ŒþÐœ×Ê20Ôª£»
·œ°ž2£ºµ×Ðœ90Ôª£¬Ã¿ÈÕÇ°5ŒþµÄÏúÊÛÁ¿Ã»ÓÐœ±Àø£¬³¬¹ý5ŒþµÄ²¿·ÖÿŒþœ±Àø20Ôª£®
£š1£©·Ö±ðÇó³öÁœÖÖÈÕÐœ·œ°žÖÐÈÕ¹€×Êy£šµ¥Î»£ºÔª£©ÓëÏúÊÛŒþÊýnµÄº¯Êý¹Øϵʜ£»
£š2£©Èôœ«ÆµÂÊÊÓΪžÅÂÊ£¬»ØŽðÏÂÁÐÎÊÌ⣺
£š¢ñ£©žùŸÝÖù׎͌£¬ÊÔ·Ö±ð¹ÀŒÆÁœÖÖ·œ°žµÄÈÕÐœX£šµ¥Î»£ºÔª£©µÄÊýѧÆÚÍûŒ°·œ²î£»
£š¢ò£©Èç¹ûÄãÒªÓŠÆžžÃ¹«ËŸµÄÏúÊÛÔ±£¬œáºÏ£š¢ñ£©ÖеÄÊýŸÝ£¬žùŸÝͳŒÆѧµÄËŒÏ룬·ÖÎöÑ¡ÔñÄÄÖÖÐœ×Ê·œ°ž±ÈœÏºÏÊÊ£¬²¢ËµÃ÷ÄãµÄÀíÓÉ£®
²é¿ŽŽð°žºÍœâÎö>>
¿ÆÄ¿£ºžßÖÐÊýѧ ÀŽÔŽ£º ÌâÐÍ£º
¡ŸÌâÄ¿¡¿ÒÑÖªº¯Êýf(x)£œx£«2x£¬g(x)£œx£«ln x£¬h(x)£œx£![]() £1µÄÁãµã·Ö±ðΪx1£¬x2£¬x3£¬Ôòx1£¬x2£¬x3µÄŽóС¹ØϵÊÇ________(ÓÉСµœŽó).
£1µÄÁãµã·Ö±ðΪx1£¬x2£¬x3£¬Ôòx1£¬x2£¬x3µÄŽóС¹ØϵÊÇ________(ÓÉСµœŽó).
²é¿ŽŽð°žºÍœâÎö>>
¿ÆÄ¿£ºžßÖÐÊýѧ ÀŽÔŽ£º ÌâÐÍ£º
¡ŸÌâÄ¿¡¿ÈçÍŒ£¬ÔÚËÄÀâ׶P-ABCDÖУ¬µ×ÃæABCDΪÕý·œÐΣ¬ÆœÃæPAD¡ÍÆœÃæABCD£¬µãMÔÚÏ߶ÎPPD//ÆœÃæMAC£¬PA=PD=![]() £¬AB=4£®
£¬AB=4£®
£šI£©ÇóÖ€£ºMΪPBµÄÖе㣻
£šII£©Çó¶þÃæœÇB-PD-AµÄŽóС£»
£šIII£©ÇóÖ±ÏßMCÓëÆœÃæBDPËù³ÉœÇµÄÕýÏÒÖµ£®

²é¿ŽŽð°žºÍœâÎö>>
°Ù¶ÈÖÂÐÅ - Á·Ï°²áÁбí - ÊÔÌâÁбí
ºþ±±Ê¡»¥ÁªÍøÎ¥·šºÍ²»ÁŒÐÅÏ¢ŸÙ±šÆœÌš | ÍøÉÏÓкŠÐÅÏ¢ŸÙ±š×šÇø | µçÐÅÕ©ÆŸÙ±š×šÇø | ÉæÀúÊ·ÐéÎÞÖ÷ÒåÓкŠÐÅÏ¢ŸÙ±š×šÇø | ÉæÆóÇÖÈšŸÙ±š×šÇø
Î¥·šºÍ²»ÁŒÐÅÏ¢ŸÙ±šµç»°£º027-86699610 ŸÙ±šÓÊÏ䣺58377363@163.com