
【题目】已知![]() 为正整数,数列
为正整数,数列![]() 满足
满足![]() ,
, ![]() ,设数列
,设数列![]() 满足
满足![]()
(1)求证:数列![]() 为等比数列;
为等比数列;
(2)若数列![]() 是等差数列,求实数
是等差数列,求实数![]() 的值;
的值;
(3)若数列![]() 是等差数列,前
是等差数列,前![]() 项和为
项和为![]() ,对任意的
,对任意的![]() ,均存在
,均存在![]() ,使得
,使得![]() 成立,求满足条件的所有整数
成立,求满足条件的所有整数![]() 的值.
的值.
【答案】(1)见解析;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】试题分析:
(1)由![]() ,可得
,可得![]() ,两边开方得
,两边开方得![]() ,于是证得数列
,于是证得数列![]() 为等比数列.(2)由(1)可得
为等比数列.(2)由(1)可得![]() ,故
,故![]() ,从而可得数列
,从而可得数列![]() 的通项公式,根据等差数列可得
的通项公式,根据等差数列可得![]() ,由此求得
,由此求得![]() 或
或![]() ,然后分别验证可得
,然后分别验证可得![]() 符合条件.(3)由题意可得有
符合条件.(3)由题意可得有![]() 成立,即
成立,即![]() 对任意的
对任意的![]() ,均存在
,均存在![]() 成立,且
成立,且![]() 为正整数,然后将
为正整数,然后将![]() 分为奇数和偶数两种情况讨论,最后可得
分为奇数和偶数两种情况讨论,最后可得![]() 时符合题意.
时符合题意.
试题解析:
(1)证明:∵![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() ,
,
![]() 数列
数列![]() 是首项为
是首项为![]() ,公比为2的等比数列.
,公比为2的等比数列.
(2)解:由(1)得![]() ,
,
∴![]() ,
,
∴![]()
![]() 数列
数列![]() 是等差数列,
是等差数列,
∴![]() ,
,
![]() ,
,
解得![]() 或
或![]() .
.
当![]() 时,
时,![]() ,是关于n的一次函数,因此数列
,是关于n的一次函数,因此数列![]() 是等差数列;
是等差数列;
当![]() 时,
时,![]() ,由于
,由于![]() ,不是常数,因此数列
,不是常数,因此数列![]() 不是等差数列.
不是等差数列.
综上可得![]() .
.
(3)解:由(2)得![]() ,
,
对任意的![]() ,均存在
,均存在![]() ,使得
,使得![]() 成立,
成立,
即有![]() ,
,
化简得![]() ,
,
当![]() 时,
时,![]() ,对任意的
,对任意的![]() ,符合题意;
,符合题意;
当![]() 时,若
时,若![]() ,则
,则![]() 不符合题意.对任意的
不符合题意.对任意的![]() ,也不符合题意.
,也不符合题意.
综上可得,当![]() ,对任意的
,对任意的![]() ,均存在
,均存在![]() ,使得
,使得![]() 成立.
成立.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
【题目】如图,已知圆O外有一点P,作圆O的切线PM,M为切点,过PM的中点N,作割线NAB,交圆于A,B两点,连接PA并延长,交圆O于点C,连续PB交圆O于点D,若MC=BC. 
(1)求证:△APM∽△ABP;
(2)求证:四边形PMCD是平行四边形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=2ln(x+2)﹣(x+1)2 , g(x)=k(x+1).
(1)求f(x)的单调区间;
(2)当k=2时,求证:对于x>﹣1,f(x)<g(x)恒成立;
(3)若存在x0>﹣1,使得当x∈(﹣1,x0)时,恒有f(x)>g(x)成立,试求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量.产品数量的分组区间为[45,55),[55,65),[65,75),[75,85),[85,95)由此得到频率分布直方图如图.则产品数量位于[55,65)范围内的频率为;这20名工人中一天生产该产品数量在[55,75)的人数是 . 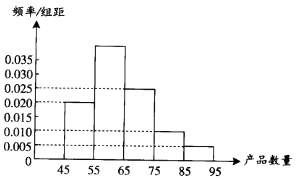
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四边形![]() 是正方形,
是正方形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 都是等边三角形,
都是等边三角形, ![]() 、
、![]() 、
、![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 、
、![]() 、
、![]() 的中点,分别以
的中点,分别以![]() 、
、![]() 、
、![]() 、
、![]() 为折痕将四个等边三角形折起,使得
为折痕将四个等边三角形折起,使得![]() 、
、![]() 、
、![]() 、
、![]() 四点重合于一点
四点重合于一点![]() ,得到一个四棱锥.对于下面四个结论:
,得到一个四棱锥.对于下面四个结论:
①![]() 与
与![]() 为异面直线; ②直线
为异面直线; ②直线![]() 与直线
与直线![]() 所成的角为
所成的角为![]()
③![]() 平面
平面![]() ; ④平面
; ④平面![]() 平面
平面![]() ;
;
其中正确结论的个数有( )

A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,等边三角形![]() 的中线
的中线![]() 与中位线
与中位线![]() 相交于
相交于![]() ,已知
,已知![]() 是
是![]() 绕
绕![]() 旋转过程中的一个图形,下列命题中,错误的是
旋转过程中的一个图形,下列命题中,错误的是

A. 恒有![]() ⊥
⊥![]()
B. 异面直线![]() 与
与![]() 不可能垂直
不可能垂直
C. 恒有平面![]() ⊥平面
⊥平面![]()
D. 动点![]() 在平面
在平面![]() 上的射影在线段
上的射影在线段![]() 上
上
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设{an}是公比大于1的等比数列,Sn为数列{an}的前n项和,已知S3=7,
且a1+3,3a2,a3+4构成等差数列.
(1)求数列{an}的通项;
(2)令![]() ,n=1,2,…,求数列{bn}的前n项和Tn .
,n=1,2,…,求数列{bn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com