
【题目】己知函数![]() ,它的导函数为
,它的导函数为![]() .
.
(1)当![]() 时,求
时,求![]() 的零点;
的零点;
(2)若函数![]() 存在极小值点,求
存在极小值点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() 是
是![]() 的零点;(2)
的零点;(2)![]()
【解析】
(1)求得![]() 时的
时的![]() ,由单调性及
,由单调性及![]() 求得结果.
求得结果.
(2)当![]() 时,
时,![]() ,易得
,易得![]() 存在极小值点,再分当
存在极小值点,再分当![]() 时和当
时和当![]() 时,令
时,令![]() ,通过研究
,通过研究![]() 的单调性及零点情况,得到
的单调性及零点情况,得到![]() 的零点及分布的范围,进而得到
的零点及分布的范围,进而得到![]() 的极值情况,综合可得结果.
的极值情况,综合可得结果.
(1)![]() 的定义域为
的定义域为![]() ,
,
当![]() 时,
时,![]() ,
,![]() .
.
易知![]() 为
为![]() 上的增函数,
上的增函数,
又![]() ,所以
,所以![]() 是
是![]() 的零点.
的零点.
(2)![]() ,
,
① 当![]() 时,
时,![]() ,令
,令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,符合题意.
上单调递增,符合题意.
令![]() ,则
,则![]() .
.
② 当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递增.
上单调递增.
又![]() ,
,![]() ,
,
所以![]() 在
在![]() 上恰有一个零点
上恰有一个零点![]() ,且当
,且当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,所以
,所以![]() 是
是![]() 的极小值点,符合题意.
的极小值点,符合题意.
③ 当![]() 时,令
时,令![]() ,得
,得![]() .
.
当![]() )时,
)时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以![]() .
.
若![]() ,即当
,即当![]() 时,
时,![]() 恒成立,
恒成立,
即![]() 在
在![]() 上单调递增,无极值点,不符合题意.
上单调递增,无极值点,不符合题意.
若![]() ,即当
,即当![]() 时,
时,![]() ,
,
所以![]() ,即
,即![]() 在
在![]() 上恰有一个零点
上恰有一个零点![]() ,且当
,且当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以![]() 是
是![]() 的极小值点,符合题意.
的极小值点,符合题意.
综上,可知![]() ,即
,即![]() 的取值范围为
的取值范围为![]() .
.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
【题目】中国国际智能产业博览会(智博会)每年在重庆市举办一届,每年参加服务的志愿者分“嘉宾”、“法医”等若干小组,![]() 年底,来自重庆大学、西南大学、重庆医科大学、西南政法大学的500名学生在重庆科技馆多功能厅参加了“志愿者培训”,如图是四所大学参加培训人数的不完整条形统计图,现用分层抽样的方法从中抽出20人作为2019年中国国际智博会服务的志愿者.
年底,来自重庆大学、西南大学、重庆医科大学、西南政法大学的500名学生在重庆科技馆多功能厅参加了“志愿者培训”,如图是四所大学参加培训人数的不完整条形统计图,现用分层抽样的方法从中抽出20人作为2019年中国国际智博会服务的志愿者.
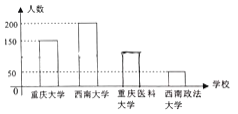
(1)分别求出从重庆大学、西南大学、重庆医科大学、西南政法大学抽出的志愿者人数;
(2)若“嘉宾”小组的2名志愿者只能从重庆医科大学或西南政法大学抽出,求这2人分别来自不同大学的概率(结果用分数表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着城市地铁建设的持续推进,市民的出行也越来越便利.根据大数据统计,某条地铁线路运行时,发车时间间隔t(单位:分钟)满足:4≤t≤15,![]() N,平均每趟地铁的载客人数p(t)(单位:人)与发车时间间隔t近似地满足下列函数关系:
N,平均每趟地铁的载客人数p(t)(单位:人)与发车时间间隔t近似地满足下列函数关系: ,其中
,其中![]() .
.
(1)若平均每趟地铁的载客人数不超过1500人,试求发车时间间隔t的值.
(2)若平均每趟地铁每分钟的净收益为![]() (单位:元),问当发车时间间隔t为多少时,平均每趟地铁每分钟的净收益最大?井求出最大净收益.
(单位:元),问当发车时间间隔t为多少时,平均每趟地铁每分钟的净收益最大?井求出最大净收益.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x﹣2)ex﹣![]() +
+![]() x,其中
x,其中![]() ∈R,e是自然对数的底数.
∈R,e是自然对数的底数.
(1)当![]() >0时,讨论函数f(x)在(1,+∞)上的单调性;
>0时,讨论函数f(x)在(1,+∞)上的单调性;
(2)若函数g(x)=f![]() (x)+2﹣
(x)+2﹣![]() ,证明:使g(x)≥0在
,证明:使g(x)≥0在![]() 上恒成立的实数a能取到的最大整数值为1.
上恒成立的实数a能取到的最大整数值为1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,过
,过![]() 作
作![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 于点
于点![]() (点
(点![]() 在
在![]() 轴上方),斜率为
轴上方),斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,且
,且![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)设椭圆![]() 的离心率为
的离心率为![]() ,当点
,当点![]() 为椭圆
为椭圆![]() 的右顶点时,
的右顶点时,![]() 的坐标为
的坐标为 ,求
,求![]() 的值.
的值.
(2)若椭圆![]() 的方程为
的方程为![]() ,且
,且![]() ,是否存
,是否存![]() 在使得
在使得![]() 成立?如果存在,求出
成立?如果存在,求出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的各项都是正数,若对于任意的正整数
的各项都是正数,若对于任意的正整数![]() ,存在
,存在![]() ,使得
,使得![]() 、
、![]() 、
、![]() 成等比数列,则称函数
成等比数列,则称函数![]() 为“
为“![]() 型”数列.
型”数列.
(1)若![]() 是“
是“![]() 型”数列,且
型”数列,且![]() ,
,![]() ,求
,求![]() 的值;
的值;
(2)若![]() 是“
是“![]() 型”数列,且
型”数列,且![]() ,
,![]() ,求
,求![]() 的前
的前![]() 项和
项和![]() ;
;
(3)若![]() 既是“
既是“![]() 型”数列,又是“
型”数列,又是“![]() 型”数列,求证:数列
型”数列,求证:数列![]() 是等比数列.
是等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(2x-4)ex+a(x+2)2(x>0,a∈R,e是自然对数的底数).
(1)若f(x)是(0,+∞)上的单调递增函数,求实数a的取值范围;
(2)当a∈![]() 时,证明:函数f(x)有最小值,并求函数f(x)的最小值的取值范围.
时,证明:函数f(x)有最小值,并求函数f(x)的最小值的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com