
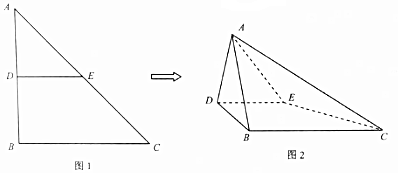
分析 (1)证明:DE⊥平面ADB,DE∥BC,可证BC⊥平面ABD,即可证明平面ABD⊥平面ABC.
(2)取DB中点O,AO⊥DB,由(1)得平面ABD⊥平面EDBC,AO⊥面EDBC,所以以O为原点,建立如图坐标系,
则A(0,0,$\sqrt{3}$),B(1,0,0),C(1,4,0),E(-1,2,0),利用平面ABC的法向量 求解.
解答 (1)证明:由题意,DE∥BC,
∵DE⊥AD,DE⊥BD,AD∩BD=D,
∴DE⊥平面ADB,∴BC⊥平面ABD;
∵$BC?\\;面ABC$面ABC,∴平面ABD⊥平面ABC;
(2)由已知可得二面角A-DE-C的平面角就是∠ADB
设等腰直角三角形ABC的直角边AB=4,则在△ADB中,AD=DB=AB=2,
取DB中点O,AO⊥DB,由(1)得平面ABD⊥平面EDBC,
∴AO⊥面EDBC,所以以O为原点,建立如图坐标系,
则A(0,0,$\sqrt{3}$),B(1,0,0),C(1,4,0),E(-1,2,0)
设平面ABC的法向量为$\overrightarrow{m}=(x,y,z)$,
$\overrightarrow{AB}=(1,0,-\sqrt{3})$,$\overrightarrow{AC}=(1,4,-\sqrt{3})$.由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AB}=x-\sqrt{3}z=0}\\{\overrightarrow{m}•\overrightarrow{AC}=x+4y-\sqrt{3}z=0}\end{array}\right.$,取$\overrightarrow{m}=(\sqrt{3},0,1)$,
$\overrightarrow{AE}=(-1,2,-\sqrt{3}$},
∴直线AE与平面ABC所成角的θ,sinθ=|cos<$\overrightarrow{m},\overrightarrow{AE}$>|=|$\frac{\overrightarrow{m}•\overrightarrow{AE}}{|\overrightarrow{AE}||\overrightarrow{m}|}$|=$\frac{\sqrt{6}}{4}$.
即直线AE与平面ABC所成角的正弦值为:$\frac{\sqrt{6}}{4}$
点评 本题考查线面垂直,考查向量法求二面角,考查学生分析解决问题的能力,属于中档题.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{{2}^{n}}$$\frac{(-1)^{n}}{{2}^{n}}$ | B. | $\frac{(-1)^{n}}{{2}^{n}}$ | C. | $\frac{(-1)^{n+1}}{{2}^{n}}$ | D. | $\frac{(-1)^{n}}{{2}^{n-1}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 1 | C. | 10 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
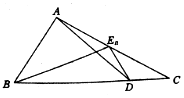 如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BD}$=3$\overrightarrow{DC}$,En(n∈N+)为边AC的一列点,满足$\overrightarrow{{E}_{n}A}$=$\frac{1}{4}$an+1$\overrightarrow{{E}_{n}B}$-(3an+2)$\overrightarrow{{E}_{n}D}$,其中实数列{an}中an>0,a1=1,则{an}的通项公式为( )
如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BD}$=3$\overrightarrow{DC}$,En(n∈N+)为边AC的一列点,满足$\overrightarrow{{E}_{n}A}$=$\frac{1}{4}$an+1$\overrightarrow{{E}_{n}B}$-(3an+2)$\overrightarrow{{E}_{n}D}$,其中实数列{an}中an>0,a1=1,则{an}的通项公式为( )| A. | 3•2n-1-2 | B. | 2n-1 | C. | 3n-2 | D. | 2•3n-1-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{\sqrt{6}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=5,b=5,A=50° | B. | a=3,b=4,A=30° | ||
| C. | a=5,b=10,A=30° | D. | a=12,b=10,A=135° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A⊆B | B. | B⊆A | C. | A∪B=R | D. | A∩B=∅ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com