
【题目】已知正方形![]() 的边长为
的边长为![]() ,将
,将![]() 沿对角线
沿对角线![]() 折起,使平面
折起,使平面![]() 平面
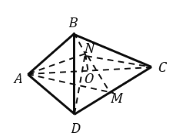
平面![]() ,得到如图所示的三棱锥
,得到如图所示的三棱锥![]() ,若
,若![]() 为
为![]() 边的中点,
边的中点,![]() 分别为
分别为![]() 上的动点(不包括端点),且
上的动点(不包括端点),且![]() ,设
,设![]() ,则三棱锥
,则三棱锥![]() 的体积取得最大值时,三棱锥
的体积取得最大值时,三棱锥![]() 的内切球的半径为_______.
的内切球的半径为_______.
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,若函数
,若函数![]() 有三个不同的零点
有三个不同的零点![]() ,
,![]() ,
,![]() (其中
(其中![]() ),则
),则![]() 的取值范围为__________.
的取值范围为__________.
【答案】![]()
【解析】如图:

![]() ,
,![]() ,作出函数图象如图所示
,作出函数图象如图所示
![]() ,
,![]() ,作出函数图象如图所示
,作出函数图象如图所示
![]()
![]() ,由
,由![]() 有三个不同的零点
有三个不同的零点
![]() ,如图
,如图
令![]()
![]()
得![]()
![]()
为满足有三个零点,如图可得
![]() ,
,![]()
![]()
![]()
点睛:本题考查了函数零点问题,先由导数求出两个函数的单调性,继而画出函数图像,再由函数的零点个数确定参量取值范围,将问题转化为函数的两根问题来求解,本题需要化归转化,函数的思想,零点问题等较为综合,有很大难度。
【题型】填空题
【结束】
17
【题目】已知等比数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足
满足![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了估计某校某次数学考试的情况,现从该校参加考试的600名学生中随机抽出60名学生,其数学成绩(百分制)均在![]() 内,将这些成绩分成六组
内,将这些成绩分成六组![]() …
…![]() ,得到如图所示的部分频率分布直方图.
,得到如图所示的部分频率分布直方图.

(1)求抽出的60名学生中数学成绩在![]() 内的人数;
内的人数;
(2)若规定成绩不小于85分为优秀,则根据频率分布直方图,估计该校参加考试的学生数学成绩为优秀的人数;
(3)试估计抽出的60名学生的数学成绩的中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,雾霾日趋严重,雾霾的工作、生活受到了严重的影响,如何改善空气质量已成为当今的热点问题,某空气净化器制造厂,决定投入生产某型号的空气净化器,根据以往的生产销售经验得到下面有关生产销售的统计规律,每生产该型号空气净化器![]() (百台),其总成本为
(百台),其总成本为![]() (万元),其中固定成本为12万元,并且每生产1百台的生产成本为10万元(总成本=固定成本+生产成本),销售收入
(万元),其中固定成本为12万元,并且每生产1百台的生产成本为10万元(总成本=固定成本+生产成本),销售收入![]() (万元)满足
(万元)满足![]() ,假定该产品销售平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品销售平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(1)求利润函数![]() 的解析式(利润=销售收入-总成本);
的解析式(利润=销售收入-总成本);
(2)工厂生产多少百台产品时,可使利润最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】填空:
(1)如果![]() ,且
,且![]() ,则
,则![]() 是第________象限角;
是第________象限角;
(2)如果![]() ,且
,且![]() ,则
,则![]() 是第________象限角;
是第________象限角;
(3)如果![]() ,且
,且![]() ,则
,则![]() 是第________象限角;
是第________象限角;
(4)如果![]() ,且
,且![]() ,则
,则![]() 是第________象限角.
是第________象限角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 是以
是以![]() 为斜边的直角三角形,
为斜边的直角三角形,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)若线段![]() 上有一个点
上有一个点![]() ,使得
,使得![]() 平面
平面![]() ,请确定点
,请确定点![]() 的位置,并说明理由;
的位置,并说明理由;
(2)若平面![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于圆周率![]() ,数学发展史上出现过许多很有创意的求法,如著名的蒲丰试验.受其启发,我们也可以通过设计下面的试验来估计
,数学发展史上出现过许多很有创意的求法,如著名的蒲丰试验.受其启发,我们也可以通过设计下面的试验来估计![]() 的值,试验步骤如下:①先请高二年级 500名同学每人在小卡片上随机写下一个实数对
的值,试验步骤如下:①先请高二年级 500名同学每人在小卡片上随机写下一个实数对![]() ;②若卡片上的
;②若卡片上的![]() 能与1构成锐角三角形,则将此卡片上交;③统计上交的卡片数,记为
能与1构成锐角三角形,则将此卡片上交;③统计上交的卡片数,记为![]() ;④根据统计数
;④根据统计数![]() 估计
估计![]() 的值.假如本次试验的统计结果是
的值.假如本次试验的统计结果是![]() ,那么可以估计
,那么可以估计![]() 的值约为( )
的值约为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经销商小王对其所经营的某一型号二手汽车的使用年数![]() (0<
(0<![]() ≤10)与销售价格
≤10)与销售价格![]() (单位:万元/辆)进行整理,得到如下的对应数据:
(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
售价 | 16 | 13 | 9.5 | 7 | 4.5 |
(Ⅰ)试求![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(附:回归方程![]() 中,
中,
(Ⅱ)已知每辆该型号汽车的收购价格为![]() 万元,根据(Ⅰ)中所求的回归方程,
万元,根据(Ⅰ)中所求的回归方程,
预测![]() 为何值时,小王销售一辆该型号汽车所获得的利润
为何值时,小王销售一辆该型号汽车所获得的利润![]() 最大.
最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com