
【题目】规定投掷飞镖3次为一轮,若3次中至少两次投中8环以上为优秀,现采用随机模拟实验的方法估计某人投掷飞镖的情况:先由计算器产生随机数0或1,用0表示该次投标未在8环以上,用1表示该次投标在8环以上;再以每三个随机数作为一组,代表一轮的结果,经随机模拟实验产生了如下20组随机数:
101 111 011 101 010 100 100 011 111 110
000 011 010 001 111 011 100 000 101 101
据此估计,该选手投掷飞镖三轮,至少有一轮可以拿到优秀的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】如图,设椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,
, ![]() 分别为椭圆
分别为椭圆![]() 的左、右顶点,
的左、右顶点, ![]() 为右焦点,直线
为右焦点,直线![]() 与
与![]() 的交点到
的交点到![]() 轴的距离为
轴的距离为![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,
, ![]() 为
为![]() 上异于点
上异于点![]() 的一点,以
的一点,以![]() 为直径作圆
为直径作圆![]() .
.
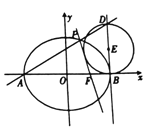
(1)求![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,证明:直线
,证明:直线![]() 与圆
与圆![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]()
(1)计算f(1)+f(0)的值;
(2)计算f(x)+f(1﹣x)的值;
(3)若关于x的不等式:f[23x﹣2﹣x+m(2x﹣2﹣x)+ ![]() ]<
]< ![]() 在区间[1,2]上有解,求实数m的取值范围.
在区间[1,2]上有解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=x+ ![]() 有如下性质:如果常数t>0,那么该函数在
有如下性质:如果常数t>0,那么该函数在 ![]() 上是减函数,在
上是减函数,在 ![]() 上是增函数.
上是增函数.
(1)已知f(x)= ![]() ,x∈[﹣1,1],利用上述性质,求函数f(x)的单调区间和值域;
,x∈[﹣1,1],利用上述性质,求函数f(x)的单调区间和值域;
(2)对于(1)中的函数f(x)和函数g(x)=﹣x﹣2a,若对任意x1∈[﹣1,1],总存在x2∈[0,1],使得g(x2)=f(x1)成立,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知具有相关关系的两个变量![]() 之间的几组数据如下表所示:
之间的几组数据如下表所示:

(1)请根据上表数据在网格纸中绘制散点图;
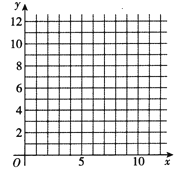
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并估计当
,并估计当![]() 时,
时, ![]() 的值;
的值;
(3)将表格中的数据看作五个点的坐标,则从这五个点中随机抽取2个点,求这两个点都在直线![]() 的右下方的概率.
的右下方的概率.
参考公式:  ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数f(x)=xa的图象经过点( ![]() ,
, ![]() ).
).
(1)求函数f(x)的解析式,并判断奇偶性;
(2)判断函数f(x)在(﹣∞,0)上的单调性,并用单调性定义证明.
(3)作出函数f(x)在定义域内的大致图象(不必写出作图过程).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy 中,椭圆G的中心为坐标原点,左焦点为F1(﹣1,0),离心率e=![]() .
.
(1)求椭圆G 的标准方程;
(2)已知直线l1:y=kx+m1与椭圆G交于 A,B两点,直线l2:y=kx+m2(m1≠m2)与椭圆G交于C,D两点,且|AB|=|CD|,如图所示.
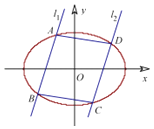
①证明:m1+m2=0;
②求四边形ABCD 的面积S 的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(x+1),g(x)=log2(3x+1).
(1)求出使g(x)≥f(x)成立的x的取值范围;
(2)当x∈[0,+∞)时,求函数y=g(x)﹣f(x)的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com