
【题目】已知数列![]() 满足:对任意
满足:对任意![]() ,都有
,都有![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() 是等比数列,求
是等比数列,求![]() 的通项公式;
的通项公式;
(3)设![]() ,
,![]() ,求证:若
,求证:若![]() 成等差数列,则
成等差数列,则![]() 也成等差数列.
也成等差数列.
科目:高中数学 来源: 题型:
【题目】某地区试行高考考试改革:在高三学年中举行5次统一测试,学生如果通过其中2次测试即可获得足够学分升上大学继续学习,不用参加其余的测试,而每个学生最多也只能参加5次测试![]() 假设某学生每次通过测试的概率都是
假设某学生每次通过测试的概率都是![]() ,每次测试时间间隔恰当,每次测试通过与否互相独立.
,每次测试时间间隔恰当,每次测试通过与否互相独立.
(1)求该学生考上大学的概率.
(2)如果考上大学或参加完5次测试就结束,记该生参加测试的次数为X,求X的概率分布及X的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元2020年春,我国湖北武汉出现了新型冠状病毒,人感染后会出现发热、咳嗽、气促和呼吸困难等,严重的可导致肺炎甚至危及生命.为了尽快遏制住病毒的传播,我国科研人员,在研究新型冠状病毒某种疫苗的过程中,利用小白鼠进行科学试验.为了研究小白鼠连续接种疫苗后出现![]() 症状的情况,决定对小白鼠进行做接种试验.该试验的设计为:①对参加试验的每只小白鼠每天接种一次;②连续接种三天为一个接种周期;③试验共进行3个周期.已知每只小白鼠接种后当天出现症状的概率均为
症状的情况,决定对小白鼠进行做接种试验.该试验的设计为:①对参加试验的每只小白鼠每天接种一次;②连续接种三天为一个接种周期;③试验共进行3个周期.已知每只小白鼠接种后当天出现症状的概率均为![]() ,假设每次接种后当天是否出现
,假设每次接种后当天是否出现![]() 症状与上次接种无关.
症状与上次接种无关.
(1)若某只小白鼠出现![]() 症状即对其终止试验,求一只小白鼠至多能参加一个接种周期试验的概率;
症状即对其终止试验,求一只小白鼠至多能参加一个接种周期试验的概率;
(2)若某只小白鼠在一个接种周期内出现2次或3次![]() 症状,则在这个接种周期结束后,对其终止试验.设一只小白鼠参加的接种周期为
症状,则在这个接种周期结束后,对其终止试验.设一只小白鼠参加的接种周期为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第十三届全国人民代表大会第二次会议和政协第十三届全国委员会第二次会议(简称两会)将分别于![]() 年
年![]() 月
月![]() 日和
日和![]() 月
月![]() 日在北京开幕.全国两会召开前夕,某网站推出两会热点大型调查,调查数据表明,网约车安全问题是百姓最为关心的热点之一,参与调查者中关注此问题的约占
日在北京开幕.全国两会召开前夕,某网站推出两会热点大型调查,调查数据表明,网约车安全问题是百姓最为关心的热点之一,参与调查者中关注此问题的约占![]() .现从参与者中随机选出
.现从参与者中随机选出![]() 人,并将这
人,并将这![]() 人按年龄分组:第
人按年龄分组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示:
,得到的频率分布直方图如图所示:
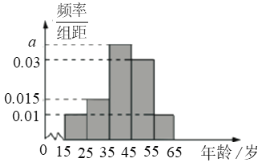
(Ⅰ)现在要从年龄较小的第![]() ,
,![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人赠送礼品,求抽取的
人赠送礼品,求抽取的![]() 人中至少有
人中至少有![]() 人年龄在第
人年龄在第![]() 组的概率;
组的概率;
(Ⅱ)把年龄在第![]() ,
,![]() ,
,![]() 组的人称为青少年组,年龄在第
组的人称为青少年组,年龄在第![]() ,
,![]() 组的人称为中老年组,若选出的
组的人称为中老年组,若选出的![]() 人中不关注网约车安全问题的人中老年人有
人中不关注网约车安全问题的人中老年人有![]() 人,问是否有
人,问是否有![]() 的把握认为是否关注网约车安全问题与年龄有关?附:
的把握认为是否关注网约车安全问题与年龄有关?附:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
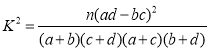 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() (
(![]() )的焦点为
)的焦点为![]() ,准线为
,准线为![]() ,若点
,若点![]() 在抛物线
在抛物线![]() 上,点
上,点![]() 在直线
在直线![]() 上,且
上,且![]() 是周长为12的等边三角形.
是周长为12的等边三角形.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)设过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,若
,若![]() ,求直线
,求直线![]() 斜率的取值范围.
斜率的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com