Question

【题目】已知a，b为常数，a0，函数．

（1）若a=2，b=1，求在（0，+∞）内的极值；

（2）①若a>0，b>0，求证：在区间[1，2]上是增函数；

②若，，且在区间[1，2]上是增函数，求由所有点形成的平面区域的面积．

Answer 1

【答案】（1），（2）①详见解析，②

【解析】

试题分析：（1）求具体函数极值问题分三步，一是求导，二是求根，三是列表，关键在于正确求出导数，即；求根时需结合定义区间进行取舍，如根据定义区间舍去负根；列表时需注意导数在对应区间的符号变化规律，这样才可得出正确结论，因为导数为零的点不一定为极值点，极值点附近导数值必须要变号，（2）①利用导数证明函数单调性，首先要正确转化，如本题只需证到在区间[1，2]上成立即可，由得只需证到在区间[1，2]上，因为对称轴在区间[1，2]上单调增，因此只需证，而这显然成立，②中条件“在区间[1，2]上是增函数”与①不同，它是要求在区间[1，2]上恒成立，结合二次函数图像可得关于不等关系，再考虑，，可得可行域.

试题解析：（1）解:2分

当时,,

令得或(舍去) 4分

当时,是减函数,

当时,是增函数

所以当时,取得极小值为6分

（2）令

①证明:二次函数的图象开口向上,

对称轴且8分

对一切恒成立.

又对一切恒成立.

函数图象是不间断的,

在区间上是增函数. 10分

②解:

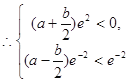即

在区间上是增函数

对恒成立.

则对恒成立.

12分

在(*)(**)的条件下,且

且恒成立.

综上,点满足的线性约束条件是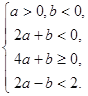14分

由所有点形成的平面区域为(如图所示),

其中

则

即的面积为. 16分