
【题目】把方程![]() 表示的曲线作为函数
表示的曲线作为函数![]() 的图象,则下列结论正确的有( )
的图象,则下列结论正确的有( )
A.![]() 的图象不经过第一象限
的图象不经过第一象限
B.![]() 在
在![]() 上单调递增
上单调递增
C.![]() 的图象上的点到坐标原点的距离的最小值为
的图象上的点到坐标原点的距离的最小值为![]()
D.函数![]() 不存在零点
不存在零点
 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】国家大力提倡科技创新,某工厂为提升甲产品的市场竞争力,对生产技术进行创新改造,使甲产品的生产节能降耗.以下表格提供了节能降耗后甲产品的生产产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨)的几组对照数据.
(吨)的几组对照数据.
|
|
|
|
|
|
|
|
|
|
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(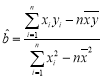 ,
,![]() )
)
(2)已知该厂技术改造前生产![]() 吨甲产品的生产能耗为
吨甲产品的生产能耗为![]() 吨,试根据(1)求出的线性回归方程,预测节能降耗后生产
吨,试根据(1)求出的线性回归方程,预测节能降耗后生产![]() 吨甲产品的生产能耗比技术改造前降低多少吨?
吨甲产品的生产能耗比技术改造前降低多少吨?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正数数列![]() 、
、![]() 满足:
满足:![]() ≥
≥![]() ,且对一切k≥2,k
,且对一切k≥2,k![]() ,
,![]() 是
是![]() 与
与![]() 的等差中项,
的等差中项,![]() 是
是![]() 与
与![]() 的等比中项.
的等比中项.
(1)若![]() ,
,![]() ,求
,求![]() ,
,![]() 的值;
的值;
(2)求证:![]() 是等差数列的充要条件是
是等差数列的充要条件是![]() 为常数数列;
为常数数列;
(3)记![]() ,当n≥2(n
,当n≥2(n![]() )时,指出
)时,指出![]() 与
与![]() 的大小关系并说明理由.
的大小关系并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设m,n是两条不同直线,α,β,γ是三个不同平面,给出下列四个命题:
①若m⊥α,n⊥α,则m∥n;②若α∥β,β∥γ,m⊥α,则m⊥γ;
③若m∥α,n∥α,则m∥n;④若m⊥α,m∥β,则α⊥β.
其中正确命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的一个焦点
)的一个焦点![]() 与抛物线
与抛物线![]() :
:![]() 的焦点重合,且离心率为
的焦点重合,且离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过焦点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,与椭圆
两点,与椭圆![]() 交于
交于![]() ,
,![]() 两点,满足
两点,满足![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
(1)求![]() 的单调性;
的单调性;
(2)若![]() ,对于任意
,对于任意![]() ,是否存在与
,是否存在与![]() 有关的正常数
有关的正常数![]() ,使得
,使得![]() 成立?如果存在,求出一个符合条件的
成立?如果存在,求出一个符合条件的![]() ;否则说明理由.
;否则说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com