
设曲线 :
: 上的点
上的点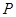 到点
到点 的距离的最小值为
的距离的最小值为 ,若
,若 ,
, ,
,
(1)求数列 的通项公式;
的通项公式;
(2)求证: ;
;
(3)是否存在常数 ,使得对
,使得对 ,都有不等式:
,都有不等式: 成立?请说明理由.
成立?请说明理由.
(1) (2)先证
(2)先证 ,累加即得证.(3)存在常数
,累加即得证.(3)存在常数 ,对
,对 ,都有不等式:
,都有不等式: 成立.(M取值不唯一)
成立.(M取值不唯一)
【解析】
试题分析:(1)设点 ,则
,则 ,∴
,∴ ,
,
∵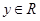 , ∴ 当
, ∴ 当 时,
时, 取得最小值
取得最小值 ,且
,且 ,
,
又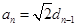 ,∴
,∴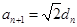 ,即
,即 , 将
, 将 代入
代入 得
得
两边平方,得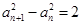 ,又
,又 ,
, ,
,
∴数列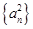 是首项为
是首项为 ,公差为
,公差为 的等差数列, ∴
的等差数列, ∴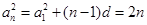 ,
,
∵ 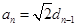
 ,∴
,∴
(2)∵ ,∴
,∴
∴ ,∴
,∴ ∴
∴ ,
,
∴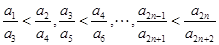
将以上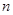 个不等式相加,得
个不等式相加,得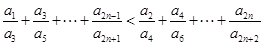 .
.
(Ⅲ)由(1)得 ,当
,当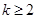 时,
时,  ,
,
∵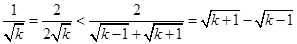 ,
,
∴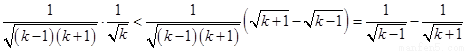 ,
,
∴ ,
,
∴
∴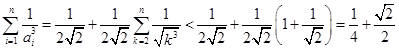 .
.
∴存在常数 ,对
,对 ,都有不等式:
,都有不等式: 成立.(M取值不唯一)
成立.(M取值不唯一)
考点:数列与不等式的综合;等差数列的通项公式;数列与函数的综合.
点评:本题考查数列的通项,考查数列与不等式的综合,考查放缩法的运用,解题的关键是根据目标,适当放缩,难度较大.


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
|
| 16 |
| 3 |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2008-2009学年浙江省杭州二中高三(下)3月月考数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com