
【题目】某旅行团按以下规定选择![]() 五个景区游玩:①若去
五个景区游玩:①若去![]() ,则去
,则去![]() ;②
;②![]() 不能同时去;③
不能同时去;③![]() 都去,或者都不去;④
都去,或者都不去;④![]() 去且只去一个;⑤若去
去且只去一个;⑤若去![]() ,则要去
,则要去![]() 和
和![]() .那么,这个旅游团最多能去的景区为_______.
.那么,这个旅游团最多能去的景区为_______.
【答案】C和D
【解析】分析:可假设⑤正确,然后根据能去不能去的关系得出矛盾,从而可得![]() 不能去,进而得
不能去,进而得![]() 都去,再判断
都去,再判断![]() 不能去即可得结果.
不能去即可得结果.
详解:先从⑤开始判断,如果去![]() ,则
,则![]() 和
和![]() 也必须去;
也必须去;
根据③,![]() 必须同去或不同去,从上面可以看出,
必须同去或不同去,从上面可以看出,![]() 已经去了,
已经去了,![]() 也必须去,因此现在可以去的地方是
也必须去,因此现在可以去的地方是![]() ;
;
结合①,若去![]() ,则
,则![]() 也必须去,因此,从①,③,⑤可以判断如果去
也必须去,因此,从①,③,⑤可以判断如果去![]() ,则
,则![]() 都必须去,与④矛盾,因此
都必须去,与④矛盾,因此![]() 不能去;
不能去;
由④得,则![]() 必须去,结合③可以判断
必须去,结合③可以判断![]() 两地是必须去的;
两地是必须去的;
再看②,![]() 两地只去一地,
两地只去一地,![]() 已经判断是必须去的,因此
已经判断是必须去的,因此![]() 不能去;
不能去;
至此,已经判断出![]() 必须去,而
必须去,而![]() 不能去,
不能去,
由①知,若去![]() ,则
,则![]() 也必须去,已经判断出
也必须去,已经判断出![]() 不能去,如果去
不能去,如果去![]() ,则与之矛盾,因此
,则与之矛盾,因此![]() 不能去,所以,该团最多能去两个地方,
不能去,所以,该团最多能去两个地方,![]() 和
和![]() ,故答案为
,故答案为![]() 和
和![]() .
.


科目:高中数学 来源: 题型:
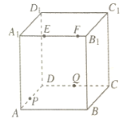
【题目】如图,正方体![]() 的棱长为4,动点E,F在棱
的棱长为4,动点E,F在棱![]() 上,动点P,Q分别在棱AD,CD上。若
上,动点P,Q分别在棱AD,CD上。若![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() 大于零),则四面体PEFQ的体积
大于零),则四面体PEFQ的体积
A.与![]() 都有关B.与m有关,与
都有关B.与m有关,与![]() 无关
无关
C.与p有关,与![]() 无关D.与π有关,与
无关D.与π有关,与![]() 无关
无关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了保护一件珍贵文物,博物馆需要在一种无色玻璃的密封保护罩内充入保护气体.假设博物馆需要支付的总费用由两部分组成:①罩内该种气体的体积比保护罩的容积少0.5立方米,且每立方米气体费用1千元;②需支付一定的保险费用,且支付的保险费用与保护罩容积成反比,当容积为2立方米时,支付的保险费用为8千元.
(1)求博物馆支付总费用y与保护罩容积V之间的函数关系式;
(2)求博物馆支付总费用的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在(0,+∞)上的函数f(x)满足下列条件:①f(x)不恒为0;②对任意的正实数x和任意的实数y都有f(xy)=yf(x).
(1)求证:方程f(x)=0有且仅有一个实数根;
(2)设a为大于1的常数,且f(a)>0,试判断f(x)的单调性,并予以证明;
(3)若a>b>c>1,且![]() ,求证:f(a)f(c)<[f(b)]2.
,求证:f(a)f(c)<[f(b)]2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是某地区2000年至2016年环境基础设施投资额![]() (单位:亿元)的折线图.
(单位:亿元)的折线图.
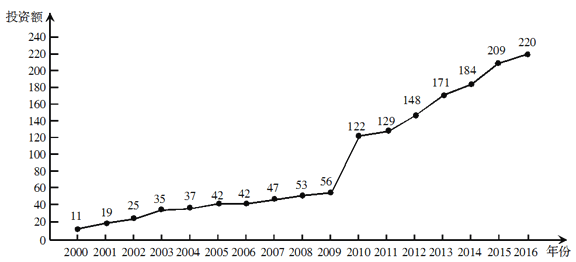
为了预测该地区2018年的环境基础设施投资额,建立了![]() 与时间变量
与时间变量![]() 的两个线性回归模型.根据2000年至2016年的数据(时间变量
的两个线性回归模型.根据2000年至2016年的数据(时间变量![]() 的值依次为
的值依次为![]() )建立模型①:
)建立模型①:![]() ;根据2010年至2016年的数据(时间变量
;根据2010年至2016年的数据(时间变量![]() 的值依次为
的值依次为![]() )建立模型②:
)建立模型②:![]() .
.
(1)分别利用这两个模型,求该地区2018年的环境基础设施投资额的预测值;
(2)你认为用哪个模型得到的预测值更可靠?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题中,正确的命题是_________.
①已知点![]() ,则
,则![]() 的面积为10.
的面积为10.
②若一个三角形,采用斜二测画法作出其直观图,则其直观图的面积是原三角形面积的![]() 倍
倍
③过点![]() 且在两坐标轴上的截距互为相反数的直线方程为
且在两坐标轴上的截距互为相反数的直线方程为![]() .
.
④直线![]() 与直线
与直线![]() 的距离是
的距离是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种新产品投放市场的100天中,前40天价格呈直线上升,而后60天其价格呈直线下降,现统计出其中4天的价格如下表:
时间 | 第4天 | 第32天 | 第60天 | 第90天 |
价格(千元) | 23 | 30 | 22 | 7 |
(1)写出价格![]() 关于时间
关于时间![]() 的函数关系式;(
的函数关系式;(![]() 表示投放市场的第
表示投放市场的第![]() 天);
天);
(2)销售量![]() 与时间
与时间![]() 的函数关系:
的函数关系:![]() ,则该产品投放市场第几天销售额最高?最高为多少千元?
,则该产品投放市场第几天销售额最高?最高为多少千元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合![]() 是非空集合
是非空集合![]() 的两个不同子集.
的两个不同子集.
(1)若![]() ,且
,且![]() 是
是![]() 的子集,求所有有序集合对
的子集,求所有有序集合对![]() 的个数;
的个数;
(2)若![]() ,且
,且![]() 的元素个数比
的元素个数比![]() 的元素个数少,求所有有序集合对
的元素个数少,求所有有序集合对![]() 的个数.
的个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com