
����Ŀ����ͼ������![]() �У�
�У� ![]() Ϊ�ȱ������Σ���ƽ��
Ϊ�ȱ������Σ���ƽ��![]() ƽ��
ƽ��![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() .
.

������֤���� ![]() ��
��
����������![]() �����Ϊ
�����Ϊ![]() ����������IJ����.
����������IJ����.
���𰸡�����֤�������������� ![]() .
.
�������������������(I) ȡ![]() ���е�Ϊ
���е�Ϊ![]() ������
������![]() ��
��![]() .���õ��������ε����ʺ;��ε����ʿ�֤��
.���õ��������ε����ʺ;��ε����ʿ�֤��![]() ,�ɴ�֤��
,�ɴ�֤��![]() ƽ��
ƽ��![]() ,��
,��![]() ,��
,��![]() .(II) ��֪
.(II) ��֪![]() �����ĸ�,���������ʽ���
�����ĸ�,���������ʽ���![]() ,���ù��ɶ����͵��������ε��������
,���ù��ɶ����͵��������ε��������![]() ��ֵ,����������.
��ֵ,����������.
�����������
֤��������ȡ![]() ���е�Ϊ
���е�Ϊ![]() ������
������![]() ��
��![]() ��
��
��![]() Ϊ�ȱ������Σ���
Ϊ�ȱ������Σ���![]() .
.
����![]() �У��ɵ��ı���
�У��ɵ��ı���![]() Ϊ���Σ���
������![]() ��
��
��![]() ����
����![]() ƽ��
ƽ��![]() ��
��
��![]() ƽ��
ƽ��![]() ����
����![]() .
.
��![]() ������
������![]() .
.
��������![]() ��
��![]() ��
��![]() ��
��
��![]() ƽ��
ƽ��![]() ������
������![]() ��
Ϊ��![]() �ĸߣ�
�ĸߣ�
��![]() ��֪
��֪![]() ��
��
![]()
![]()
![]() ��
��
��![]() .
.
�ɣ���֪![]() ��
��![]() ����
����![]() .
.
![]() .
.
��![]() ����֪
����֪![]() ƽ��
ƽ��![]() ����
����![]() ��
��
���![]() .
.
��![]() ��
��![]() ��
��![]() ��
��
ȡ![]() ���е�
���е�![]() ������
������![]() ����
����![]() ��
��![]() ��
��
��![]()
![]() .
.
������![]() �IJ����Ϊ
�IJ����Ϊ![]() .
.
�����͡������
��������
20
����Ŀ����֪Բ![]() ������Բ
������Բ![]() ��
�� ![]() ������������������㣬��
������������������㣬��![]() ��
�� ![]() ��
�� ![]() ����Բ
����Բ![]() �ϵ����㣬������
�ϵ����㣬������![]() �����࣬��
�����࣬��![]() ��ƽ������
��ƽ������![]() ���ϣ�
���ϣ� ![]() .
.
��������Բ![]() �ķ��̣�
�ķ��̣�
����֤����ֱ��![]() ������.
������.
���𰸡�����![]() .����ֱ��
.����ֱ��![]() ������
������![]() .
.
�������������������(I)����Բ�İ뾶����֪ ![]() ,��
,��![]() ,�ɴ������Բ����.(II)���ֱ��
,�ɴ������Բ����.(II)���ֱ��![]() �ķ���,����ֱ�߷�������Բ����,д��Τ�ﶨ��,д��
�ķ���,����ֱ�߷�������Բ����,д��Τ�ﶨ��,д��![]() ��б�ʲ����,�ɴ����ֱ��
��б�ʲ����,�ɴ����ֱ��![]() ������
������![]() .
.
�����������
����Բ![]() ��
��![]() �ύ��
�ύ��![]() ��Ϊ��Բ�Ľ��㣬Բ
��Ϊ��Բ�Ľ��㣬Բ![]() ��
��![]() �ύ��
�ύ��![]() ��Ϊ��Բ�����������㣬����
��Ϊ��Բ�����������㣬����![]() ��
�� ![]() .�Ӷ�
.�Ӷ�![]() ��
��
�����Բ![]() �ķ���Ϊ��
�ķ���Ϊ�� ![]() .
.
������ֱ��![]() �ķ���Ϊ
�ķ���Ϊ![]() .
.
��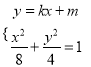 ����ȥ
����ȥ![]() ��
��![]() .
.
��![]() ��
�� ![]() ����
����![]() ��
�� ![]() .
.
ֱ��![]() ��б��
���![]()
![]() ��
��
ֱ��![]() ��б��
���![]()
![]() .
.
![]()
![]()
![]()
![]() .
.
��![]() ��ƽ������
��ƽ������![]() ���ϣ���
���ϣ���![]() .����Ϊ
.����Ϊ![]() ������
������![]() ��
��
����![]() .
.
��ˣ�ֱ��![]() ������
������![]() .
.
[�㾦]��С����Ҫ������Բ���̵����,����Բ����Բ��λ�ù�ϵ,����ֱ����Բ����λ�ù�ϵ. �漰ֱ������Բ�Ļ��������У���1��λ�ù�ϵ���ж�.��2���ҳ������е�����.��3���켣����.��4����ֵ����ֵ��������Χ����.��5������������.����˼�뷽���ͼ����У���1���������.��2�����귨.��3������ϵ����ϵ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һͬѧ�ڵ����д�����ɸ�Ȧ:��������������������������������ɸ�Ȧ���˹��ɼ�����ȥ���õ�һϵ�е�Ȧ����ô��ǰ2012��Ȧ�еġ�ĸ����� �� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2018��6��14�գ��ڶ�ʮһ�����籭���������ڶ���˹�����Ļ.Ϊ���˽�ϲ�������˶��Ƿ����Ա��йأ�ij����̨�����ȡ100�����ڽ���ͳ�ƣ��õ�����![]() ������.
������.

��1����![]() �������������������ж��ܷ��ڷ�����ĸ��ʲ�����0.001��ǰ������Ϊϲ�������˶����Ա��йأ�
�������������������ж��ܷ��ڷ�����ĸ��ʲ�����0.001��ǰ������Ϊϲ�������˶����Ա��йأ�
��2���ڲ�ϲ�������˶��Ĺ����У����Ա�ֱ��÷ֲ�����ķ�ʽ��ȡ6�ˣ��ٴ���6���������ȡ2�˲μ�һ̨��̸��Ŀ������2��������һλ���Եĸ���.
![]()

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�ڽ��ڡ�O������A����O����ǮEP��CB ���ӳ�����P����֪��PAB=25�㣮 
��1����BC�ǡ�O��ֱ�������D�Ĵ�С��
��2������DAE=25�㣬��֤��DA2=DCBP��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������費ͬ��������4�費ͬ��õ�廨�ڷ�����ͼͼ���е�1��2��3��4��5��6��7��ʾ��λ���ϣ����������������ܷ���һ��ֱ���ϣ���ͬ�İڷŷ���Ϊ�� �� 
A.2680��
B.4320��
C.4920��
D.5140��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���м��������༶������ѧ���ԣ����մ��ڵ���85��Ϊ���㣬85������Ϊ������ͳ�Ƴɼ��õ����µ�������.
| ���� | ������ | �ܼ� |
�װ� | 10 | ||
�Ұ� | 30 | ||
�ܼ� | 105 |
��֪��ȫ��105���������ȡ1��Ϊ����ĸ���Ϊ![]() .
.
(1)�����������������������������Լ���������ϣ�
(2)���������������ݣ�����95%�Ŀɿ���Ҫ���ܷ���Ϊ���ɼ���༶�й�ϵ����
�ο���ʽ��![]()
P(K2��k0) | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ú졢�ơ������ס���������ɫͿ����ͼ��ʾ���ĸ������ڣ�ÿ������Ϳһ����ɫ��������������Ϳ��ͬ����ɫ��������ɫ���Է���ʹ�ã�����___________�ֲ�ͬ��Ϳɫ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x��=x2��a|x��1|+b��a��0��b����1��
��1����b=0��a��2����f��x��������[0��2]�ڵ���Сֵm��a����
��2����f��x��������[0��2]�ڲ�ͬ�����ǡ������������������[0��1������1��2]�ڸ�һ������a��b��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ��չ��ʽ�У��ڶ�����������Ķ���ʽϵ���ɵȲ�������
��չ��ʽ�У��ڶ�����������Ķ���ʽϵ���ɵȲ�������
��1����![]() ��ֵ��
��ֵ��
��2����չ��ʽ���Ƿ��г����Ϊʲô��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com