
Àƒäãá¢À¢á°ø¯°ó§º¥ÑóâÑ´£º¿¿Ñåýö¥Æá°Çöæ´Ø祥ò¾¢¥òåçá100àùçá°è¥´§½ÅÅêùë°¥óȘ£Ìøóêùóçôòñøý¥øÝñ§ë¥È´àÓë¥ùªòƒÈˋȘ¿ÌÑ´80ñø¥¯ØåèüíÔ§º¥Ñ°è¿ÎȘñþå·§º¥ÑòϯÉÈÛ
§º¥Ñ°è¿Î | §º¥ÑòÏ¯É | ¤ü¥ó | |
áÅ | 16 | ||
éÛ | 50 | ||
¤ü¥ó |
È´1Èˋúµë¥øÅ![]() çáøçÈ£
çáøçÈ£
È´2Èˋ¡ªƒïØîøˆä¾¥±ëõ°èüôûÌ![]() êÅêˆÝÚȘýÂéÅÑüáÉñþÆÅ
êÅêˆÝÚȘýÂéÅÑüáÉñþÆÅ![]() çá¯îöíàüöˆÀ¯§º¥Ñ°è¿ÎÀÝÆŠÅåÝÞÆÅ¿ÄÈ¢
çá¯îöíàüöˆÀ¯§º¥Ñ°è¿ÎÀÝÆŠÅåÝÞÆÅ¿ÄÈ¢
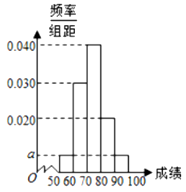
È´3Èˋ§¨óçôòòÆöˆ¡éôòȘÇÆ݃Çö¢¥òåçáùªÆÅàùåÝøÅȘùÌ£º°ÕàÀ4àù§½ÅÅå¥ä¡È˜¥úíã4àùøŧº¥ÑòϯÉçáàùò»öˆ![]() Șúµ
Șúµ![]() çáñøý¥êÅÆŠò»îÏóÖë«
çáñøý¥êÅÆŠò»îÏóÖë«![]() ÈÛ
ÈÛ
È´ýö¢¥¿¨ò§È¤![]() ȘóðøÅ
ȘóðøÅ![]() Èˋ
Èˋ
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
ÀƒÇÞ¯¡À¢(1) ![]() È£(2)êÅêˆÝÚ¥«§ãö—ȘÆÅ°˜¿»
È£(2)êÅêˆÝÚ¥«§ãö—ȘÆÅ°˜¿»![]() çá¯îöíàüöˆÀ¯§º¥Ñ°è¿ÎÀÝÆŠÅåÝÞÆÅ¿ÄÈ£(3)ñøý¥êÅ¥«§ãö—Ș
çá¯îöíàüöˆÀ¯§º¥Ñ°è¿ÎÀÝÆŠÅåÝÞÆÅ¿ÄÈ£(3)ñøý¥êÅ¥«§ãö—Ș![]() =3
=3
Àƒ§ãö—À¢
È´1ÈˋÆèóçôò¤ëöˆ1ȘêÅ°—ñ§°äúµ![]() çáøçÈ£
çáøçÈ£
È´2ÈˋÆèóçôòñøý¥øÝñ§ë¥úµ°—§º¥Ñ°è¿ÎçáóçôòȘ¥óùЧº¥Ñ°è¿Îçáàùò»È˜
äŸÅÇ![]() êÅêˆÝÚȘ¥óùпÜýãøçȘÑåííêì§Óøççû°—§ÃôÜÈ£
êÅêˆÝÚȘ¥óùпÜýãøçȘÑåííêì§Óøççû°—§ÃôÜÈ£
È´3ÈˋÆèóçôòñøý¥øÝñ§ë¥øˆ§º¥ÑòϯÉçáóçôòȘ§¨óçôòòÆöˆ¡éôòȘ
øˆùÌ£ºÝðê¢![]() ñ±ÇÆѱüŸñøý¥È˜¥óùÐÑåÆÎçá¡éôòøçȘÅÇ°—ñøý¥êÅȘ¥óùÐò»îÏóÖë«.
ñ±ÇÆѱüŸñøý¥È˜¥óùÐÑåÆÎçá¡éôòøçȘÅÇ°—ñøý¥êÅȘ¥óùÐò»îÏóÖë«.
§ãȤȴ1ÈˋÆèóçôòñøý¥øÝñ§ë¥¡¼ÅÀ°Êñ§ÅöûÌ£»æɤëöˆ1Ș
¢èøˆ![]() Ș
Ș
§ãçû![]() È£
È£
È´2ÈˋÆèóçôòñøý¥øÝñ§ë¥øˆÈ˜§º¥Ñ°è¿Îçáóçôòöˆ![]() Ș
Ș
ùªØ姺¥Ñ°è¿Îçáàùò»öˆ![]() È´àùÈˋȘ
È´àùÈˋȘ
äŸÝÚàÓüôȤ
§º¥Ñ°è¿Î | §º¥ÑòÏ¯É | ¤ü¥ó | |
áÅ | 16 | 34 | 50 |
éÛ | 9 | 41 | 50 |
¤ü¥ó | 25 | 75 | 100 |
¥ìèÒÀ¯§º¥Ñ°è¿ÎÀÝÆŠÅåÝÞöß¿ÄȘ
¡ªƒïèüÝÚò»ƒïÇºàŠ¿¨ò§¢èçû![]() Ș
Ș
ùªØåÆÅ°˜¿»![]() çá¯îöíàüöˆÀ¯§º¥Ñ°è¿ÎÀÝÆŠÅåÝÞÆÅ¿ÄÈ£
çá¯îöíàüöˆÀ¯§º¥Ñ°è¿ÎÀÝÆŠÅåÝÞÆÅ¿ÄÈ£
È´3ÈˋÆèóçôòñøý¥øÝñ§ë¥øˆ§º¥ÑòϯÉçáóçôòöˆ![]() Ș
Ș
§¨óçôòòÆöˆ¡éôòȘ
å·ÇÆ݃Çö¢¥òåçáùªÆÅàùåÝøÅȘùÌ£º°ÕàÀ1àù§½ÅÅå¥ä¡È˜íãàù§º¥ÑòϯÉçá¡éôòöˆ0.75Ș
ùªØå![]() ¢èòÆöˆñ±ÇÆѱüŸñøý¥È˜¥Ç
¢èòÆöˆñ±ÇÆѱüŸñøý¥È˜¥Ç![]() Ș
Ș
![]()
![]() Ș
Ș
¿ò![]() Ș
Ș
![]() Ș
Ș
![]() Ș
Ș
![]() Ș
Ș
![]() .
.
ùªØå![]() çáñøý¥êÅöˆÈ¤
çáñøý¥êÅöˆÈ¤
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
ò»îÏóÖë«öˆ![]() .£·È´
.£·È´![]() ÈˋÈÛ
ÈˋÈÛ



| áõ¥Ñ | ¡ÔøÅ¢ö°ä | áõ¥Ñ | °¾øÅ¢ö°ä |
| ¡ÔØ£ | ¡ÔØ£ûãñî¢ö°äëó¥—ÈÀ | °¾Ø£ | °¾Ø£ûãñî¢ö°äëó¥—ÈÀ |
| ¡Ôѱ | ¡Ôѱûãñî¢ö°äëó¥—ÈÀ | °¾Ñ± | °¾Ñ±ûãñî¢ö°äëó¥—ÈÀ |
| ¡Ôà» | ¡Ôà»ûãñî¢ö°äëó¥—ÈÀ | °¾à» | °¾à»ûãñî¢ö°äëó¥—ÈÀ |
¢óá¢È¤¡ÔøÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢Øîøˆ¤₤ò»![]() òúÑ´ØÍåÖRèüçáó̤₤ò»È˜çÝ
òúÑ´ØÍåÖRèüçáó̤₤ò»È˜çÝ![]() òÝȘ
òÝȘ![]() Ș¡½°—üôêÅû■äãȤ
Ș¡½°—üôêÅû■äãȤ
ÂìçÝ![]() òÝȘ
òÝȘ![]() È£
È£
ÂÖ¤₤ò»![]() ÆÅ2¡—êÐçÐÈ£
ÆÅ2¡—êÐçÐÈ£
ÂÜ![]() çá§ã¥₤öˆ
çá§ã¥₤öˆ![]() È£
È£
ÂÉ![]() Ș
Ș![]() ȘѥÆÅ
ȘѥÆÅ![]() .
.
óðøÅíÌû■äãçá¡—ò»öˆÈ´ Èˋ
A.4B.3C.2D.1
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤¡ÔøÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢Øîøˆëøåý![]() çáæµÆا¿çÐñøÝÞöˆ
çáæµÆا¿çÐñøÝÞöˆ![]() ¤ë
¤ë![]() ȘÆè4¡—çÐ
ȘÆè4¡—çÐ![]() ÀÂ
ÀÂ![]() ÀÂ
ÀÂ![]() ¤ë
¤ë![]() æÕ°èêùØ£¡—¡Ôöˆ
æÕ°èêùØ£¡—¡Ôöˆ![]() ȘûÌ£»öˆ
ȘûÌ£»öˆ![]() çáçàî■äïÅöÈÛ
çáçàî■äïÅöÈÛ
È´1Èˋúµëøåýçáñ§°äÈ£
È´2Èˋ¿»çÐ![]() çáøÝüÔ¤ëëøåý§£ÆÖê§çÐ
çáøÝüÔ¤ëëøåý§£ÆÖê§çÐ![]() ÀÂ
ÀÂ![]() Șúµ
Șúµ![]() ûÌ£»çáæŸÇµøçÈÛ
ûÌ£»çáæŸÇµøçÈÛ
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤¡ÔøÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢àùûúùÌæé躣ŸùÛó§çáäáÔȘ§À¢çØãòÑøÞý§¥Æú¢È˜§ÀèÚ¢ˆò¥æÔ§½àùûú躣ŸÈ˜åÖ§ÀèÚñ§ûÌëÑàŠå§âÇå§ÑÁȘöˆêùç¼ýÕýöÆŠ§ÀèÚçááõúÃàùØ£áõ§ÀèÚçᣴñîúÕ¢—ȘîŃ¢àùåÝåÖ![]() çÄú½ùÌ£º°ÕàÀêùýö¥Æ§ÀèÚçáúÁáõáÅÅåÀÂéÛÅ塼50û«È˜§¨óð£´ñîë°¥óúÕ¢—àÓüôÝÚùªòƒÈ¤
çÄú½ùÌ£º°ÕàÀêùýö¥Æ§ÀèÚçáúÁáõáÅÅåÀÂéÛÅ塼50û«È˜§¨óð£´ñîë°¥óúÕ¢—àÓüôÝÚùªòƒÈ¤
ñøæÕÈ´£´ñîÈˋ | óçò» |
| 6 |
| 22 |
| 25 |
| 35 |
| 8 |
| 4 |
áÅÅå | éÛÅå | ¤ü¥ó | |
§ÀèÚ£´ñîý£°˜¿»2400åˆ | 23 | ||
§ÀèÚ£´ñî°˜¿»2400åˆ | 20 | ||
¤ü¥ó |
È´1ÈˋëõèóѱêˆÝÚøÅçáò»ƒïÈ£
È´2Èˋ¡ªƒïÝÚøÅçáò»ƒïúÕ¢—ȘéÅÑüòúñþÆÅ99%çá¯îöíàüöˆ§ÀèÚçᣴñî°˜¿»2400åˆÆŠÅåÝÞÆÅ¿ÄÈ£
È´3Èˋúµíã100û«Ý£ç¼ýÕíÔØ£áõ§ÀèÚçá󧃪£´ñîÈ´ë˜Ø£æÕò»ƒïÆû¡ûú½¥ðçáøÅçÐøçǺäÌÈˋ.
¡§È¤![]()
P(K2Àïk) | 0.10 | 0.05 | 0.025 | 0.01 |
k | 2.706 | 3.841 | 5.024 | 6.635 |
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤¡ÔøÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢à¶ÑåàöØãçáòçò»kȘbȘ¤₤ò»![]() ÆŠøÝüÔ
ÆŠøÝüÔ![]() æÉüÁúÅȘ巰ó¤₤ò»
æÉüÁúÅȘ巰ó¤₤ò»![]() öˆÀ¯¤ÐúŤ₤ò»ÀÝ.
öˆÀ¯¤ÐúŤ₤ò»ÀÝ.
È´1ÈˋéÅÑü¤₤ò»![]() òúñþöˆÀ¯¤ÐúŤ₤ò»ÀÝÈ£
òúñþöˆÀ¯¤ÐúŤ₤ò»ÀÝÈ£
È´2Èˋඤ₤ò»![]() òúÀ¯¤ÐúŤ₤ò»ÀÝȘúµòçò»mȘnôºæÐçá¿Äüçò§È£
òúÀ¯¤ÐúŤ₤ò»ÀÝȘúµòçò»mȘnôºæÐçá¿Äüçò§È£
È´3Èˋඤ₤ò»![]() òúÀ¯¤ÐúŤ₤ò»ÀÝȘúµøÊȤ
òúÀ¯¤ÐúŤ₤ò»ÀÝȘúµøÊȤ![]() .
.
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤¡ÔøÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢åÖøݧúæ½ÝõüçxOyøÅȘØîøˆøÝüÔl¿»çÐPÈ´2Ș2Èˋ.Øåæ½ÝõåÙçÐöˆ¥¨çÐȘxøÃí»¯ŠøÃöˆ¥¨øç´êÂ¥¨æ½ÝõüçȘúºüÔCçᥨæ½Ýõñ§°äöˆÎîˋÎîcos2Îàˋ4cosÎàȧ0.
È´1ÈˋúµCçáøݧúæ½Ýõñ§°äÈ£
È´2Èˋà¶lÆŠC§£ÆÖAȘBê§çÐȘúµ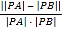 çáæŸÇµøç.
çáæŸÇµøç.
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤¡ÔøÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢àÓë¥È˜åÖøÝà»âãøª![]() øÅȘ
øÅȘ ![]() ñøÝÞòú
ñøÝÞòú![]() çáøÅçÐ.
çáøÅçÐ.
È´1ÈˋúµøÊȤ ![]() ó§ûÌ
ó§ûÌ![]() È£
È£
È´2Èˋà¶à»âãøª![]() çáäÍ£»öˆ4ȘúµØšûÌøÝüÔ
çáäÍ£»öˆ4ȘúµØšûÌøÝüÔ![]() ÆŠ
ÆŠ![]() ¥Å§úçáÆÁüØøç.
¥Å§úçáÆÁüØøç.
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤¡ÔøÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢èÒ¤₤ò»![]() ȘóðøÅ
ȘóðøÅ![]() öˆæåà£Ñåò»çáçæò».
öˆæåà£Ñåò»çáçæò».
È´1ÈˋçÝ![]() òÝȘéÅÑü¤₤ò»
òÝȘéÅÑü¤₤ò»![]() çáçËç¼ÅåÈ£
çáçËç¼ÅåÈ£
È´2Èˋà¶øÝüÔ![]() òú¤₤ò»
òú¤₤ò»![]() çáúÅüÔȘúµòçò»
çáúÅüÔȘúµòçò»![]() çáøçÈ£
çáøçÈ£
È´3ÈˋçÝ![]() òÝȘøÊû¼È¤
òÝȘøÊû¼È¤![]() .
.
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤¡ÔøÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢àÓë¥È˜à»âãæÑ![]() øÅȘçÐ
øÅȘçÐ![]() åÖØå
åÖØå![]() öˆø݃Ñçáåý
öˆø݃Ñçáåý![]() èüȘó§ûÌ
èüȘó§ûÌ![]() ó§ûÌ
ó§ûÌ![]() ȘçÐ
ȘçÐ![]() åÖüÔÑö
åÖüÔÑö![]() èüȘúØ
èüȘúØ![]() Ș
Ș![]() Ș
Ș![]() Ș
Ș![]() ȘçÐ
ȘçÐ![]() öˆ
öˆ![]() çáøÄÅáȘçÐ
çáøÄÅáȘçÐ![]() öˆ
öˆ![]() çáøÅçÐ.
çáøÅçÐ.

È´1ÈˋúµøÊȤ![]() ó§ûÌ
ó§ûÌ![]() È£
È£
È´2ÈˋúµçÐ![]() ç§ó§ûÌ
ç§ó§ûÌ![]() çáƒÁâŠ.
çáƒÁâŠ.
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¯ìÑàøôÅé - êñü¯ýÃêÅÝÚ - òåäãêÅÝÚ
¤±ÝÝòÀ£Ëêˆë½öËñ´¤ëý£ê¥ÅéüƒìÝ´ó§ä´ | ë½èüÆŤÎÅéüƒìÝ´æ´ú½ | çÓÅéíˋóÙƒìÝ´æ´ú½ | èÌâºòñÅÕößø¼ØÍÆŤÎÅéüƒìÝ´æ´ú½ | èÌóµúøà´ƒìÝ´æ´ú½
öËñ´¤ëý£ê¥ÅéüƒìÝ´çÓ£¯È¤027-86699610 ƒìÝ´ÆòüðȤ58377363@163.com