
【题目】已知平面四边形MNPQ中,MN=![]() ,MP=1,MP⊥MN,PQ⊥QM.
,MP=1,MP⊥MN,PQ⊥QM.
(Ⅰ)若PQ=![]() ,求NQ的值;
,求NQ的值;
(Ⅱ)若∠MQN=30°,求sin∠QMP的值.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() .
.
【解析】
(Ⅰ)由题意可得∠QMN=150,根据余弦定即可求出,
(Ⅱ)∠QMP=θ,由题意可得QM,∠MNQ,在△MNQ中,由正弦定理结合三角恒等变换整理可得tanθ,再根据同角三角函数的基本关系,即可求出
解:(Ⅰ)如图:∵MN=![]() ,MP=1,MP⊥MN,PQ⊥QM,
,MP=1,MP⊥MN,PQ⊥QM,
∴PQ=![]() =
=![]() ,
,
∴sin∠QMP=![]() =
=![]() ,
,
∴∠QMP=60°,
∴QM=![]() PM=
PM=![]() ,
,
∴∠QMN=150°,
由余弦定理可得NQ2=QM2+MN2﹣2MNQMcos∠QMN=![]() +3﹣2×
+3﹣2×![]() ×
×![]() ×(﹣
×(﹣![]() )=
)=![]() ,
,
∴NQ=![]() ,
,
(2):∵MN=![]() ,MP=1,MP⊥MN,PQ⊥QM
,MP=1,MP⊥MN,PQ⊥QM
设∠QMP=θ,由题意可得QM=cosθ,∠MNQ=60°﹣θ,
在△MNQ中,由正弦定理可得![]() =
=![]() ,
,
即![]() =2
=2![]() ,
,
整理可得tanθ=![]() ,
,
∵sin2θ+cos2θ=1,
![]() ,
,
故sin∠QMP=![]() .
.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:
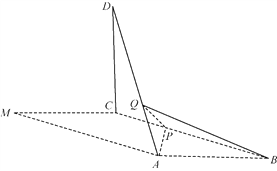
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为折痕将△
为折痕将△![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,且
的位置,且![]() .
.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)![]() 为线段
为线段![]() 上一点,
上一点,![]() 为线段
为线段![]() 上一点,且
上一点,且![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=mx3+x﹣sinx(m∈R).
(1)当m=0时,(i)求y=f(x)在(![]() ,f(
,f(![]() ))处的切线方程;
))处的切线方程;
(ii)证明:f(x)<ex;
(2)当x≥0时,函数f(x)单调递减,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在底面是菱形的四棱锥![]() 中,
中,![]() .
.
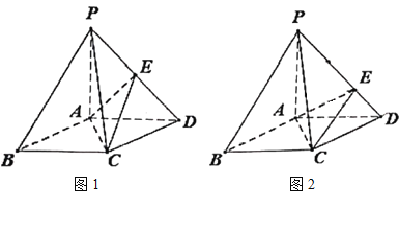
(1)证明:![]() 平面
平面![]() ;
;
(2)点![]() 在棱
在棱![]() 上.
上.
①如图1,若点![]() 是线段
是线段![]() 的中点,证明:
的中点,证明:![]() 平面
平面![]() ;
;
②如图2,若![]() ,在棱
,在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?证明你的结论.
?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 过点A(﹣1,
过点A(﹣1,![]() ),B(
),B(![]() ),F为椭圆C的左焦点.
),F为椭圆C的左焦点.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若点B为直线l1:x+y+2=0与直线l2:2x﹣y+4=0的交点,过点B的直线1与椭圆C交于D,E两点,求△DEF面积的最大值,以及此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,直线l的极坐标方程为ρcosθ=4,曲线C的极坐标方程为ρ=2cosθ+2sinθ,以极点为坐标原点O,极轴为x轴的正半轴建立直角坐标系,射线l':y=kx(x≥0,0<k<1)与曲线C交于O,M两点.
(Ⅰ)写出直线l的直角坐标方程以及曲线C的参数方程;
(Ⅱ)若射线l′与直线l交于点N,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了引导居民合理用电,国家决定实行合理的阶梯电价,居民用电原则上以住宅为单位(一套住宅为一户).

某市随机抽取10户同一个月的用电情况,得到统计表如下:

(1)若规定第一阶梯电价每度0.5元,第二阶梯超出第一阶梯的部分每度0.6元,第三阶梯超出第二阶梯每度0.8元,试计算![]() 居民用电户用电410度时应交电费多少元?
居民用电户用电410度时应交电费多少元?
(2)现要在这10户家庭中任意选取3户,求取到第二阶梯电量的户数的分布列与期望;
(3)以表中抽到的10户作为样本估计全市居民用电,现从全市中依次抽取10户,若抽到![]() 户用电量为第一阶梯的可能性最大,求
户用电量为第一阶梯的可能性最大,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com