
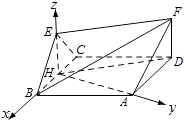
【题目】如图,菱形ABCD与正三角形BCE的边长均为2,它们所在平面互相垂直,FD⊥平面ABCD,且FD= ![]() .
.
(I)求证:EF∥平面ABCD;
(Ⅱ)若∠CBA=60°,求二面角A﹣FB﹣E的余弦值.
【答案】解:(Ⅰ)如图,过点E 作 EH⊥BC于H,连接HD, 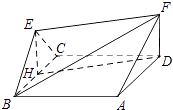
∴EH= ![]() .
.
∵平面ABCD⊥平面BCE,EH平面BCE,
平面ABD∩平面BCE=BC,
∴EH⊥平面ABCD,
又∵FD⊥平面ABCD,FD= ![]() ,
,
∴FD∥EH.FD=EH
∴四边形EHDF 为平行四边形.
∴EF∥HD
∵EF平面ABCD,HD平面ABCD,
∴EF∥平面ABCD
(Ⅱ)连接HA 由(Ⅰ),得H 为BC 中点,
又∠CBA=60°,△ABC 为等边三角形,
∴AH⊥BC,
分别以HB,HA,HE 为x,y,z 轴建立如图所示的空间直角坐标系H﹣xyz.
则 B(1,0,0),F(﹣2, ![]() ,
, ![]() ),E(0,0,
),E(0,0, ![]() ),A(0,
),A(0, ![]() ,0)
,0)![]() =(﹣3,
=(﹣3, ![]() ,
, ![]() ),
), ![]() =(﹣1,
=(﹣1, ![]() ,0),
,0), ![]() =(﹣1,0,
=(﹣1,0, ![]() ),
),
设平面EBF 的法向量为 ![]() =(x,y,z).
=(x,y,z).
由 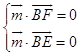 得
得 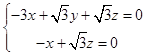
令z=1,得 ![]() =(
=( ![]() ,2,1).
,2,1).
设平面ABF的法向量为 ![]() =(x,y,z).
=(x,y,z).
由 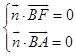 得
得 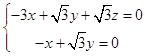
令y=1,得 ![]() =(
=( ![]() ,1,2)
,1,2)
cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∵二面角A﹣FB﹣E是钝二面角,
∴二面角A﹣FB﹣E的余弦值是﹣ ![]() .
.
【解析】(I)根据线面平行的判定定理即可证明EF∥平面ABCD;(Ⅱ),建立空间坐标系,利用向量法即可求二面角A﹣FB﹣E的余弦值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设f(x)=x ln x﹣ax2+(2a﹣1)x,a∈R.
(Ⅰ)令g(x)=f′(x ),求 g(x)的单调区间;
(Ⅱ)当a≤0时,直线 y=t(﹣1<t<0)与f(x)的图象有两个交点A(x1 , t),B(x2 , t),且x1<x2 , 求证:x1+x2>2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4cosxsin(x+ ![]() )+m(m∈R),当x∈[0,
)+m(m∈R),当x∈[0, ![]() ]时,f(x)的最小值为﹣1.
]时,f(x)的最小值为﹣1.
(Ⅰ)求m的值;
(Ⅱ)在△ABC中,已知f(C)=1,AC=4,延长AB至D,使BC=BD,且AD=5,求△ACD的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为( ) (参考数据: ![]() ≈1.732,sin15°≈0.2588,sin7.5°≈0.1305)
≈1.732,sin15°≈0.2588,sin7.5°≈0.1305)
A.12
B.24
C.36
D.48
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x2+ax,g(x)=ex , a∈R且a≠0,e=2.718…,e为自然对数的底数.
x2+ax,g(x)=ex , a∈R且a≠0,e=2.718…,e为自然对数的底数.
(Ⅰ)求函数h(x)=f(x)g(x)在[﹣1,1]上极值点的个数;
(Ⅱ)令函数p(x)=f'(x)g(x),若a∈[1,3],函数p(x)在区间[b+a﹣ea , +∞]上均为增函数,求证:b≥e3﹣7.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答题。
(1)已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线 ![]() x﹣
x﹣ ![]() y+12=0相切.求椭圆C的方程;
y+12=0相切.求椭圆C的方程;
(2)已知⊙A1:(x+2)2+y2=12和点A2(2,0),求过点A2且与⊙A1相切的动圆圆心P的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形ABCD为正方形,四边形ABEF为直角梯形,且AF∥BE,AB⊥BE,平面ABCD∩平面ABEF=AB,AB=BE=2AF=2. (Ⅰ)求证:AC∥平面DEF;
(Ⅱ)若二面角D﹣AB﹣E为直二面角,
( i)求直线AC与平面CDE所成角的大小;
( ii)棱DE上是否存在点P,使得BP⊥平面DEF?若存在,求出 ![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.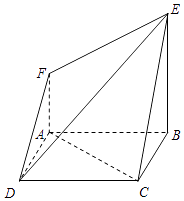
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com