
分析 不妨设a≥b≥c,通过排序不等式推出a2(b+c-a)+b2(c+a-b)+c2(a+b-c)≤ba(b+c-a)+cb(c+a-b)+ac(a+b-c),a2(b+c-a)+b2(c+a-b)+c2(a+b-c)≤ca(b+c-a)+ab(c+a-b)+bc(a+b-c)即可推出结果.
解答 证明:不妨设a≥b≥c,可得ac-bc≤a2-b2,即a(b+c-a)≤b(c+a-b),
容易验证a(b+c-a)≤b(c+a-b)≤c(a+b-c),
由排序不等式可得a2(b+c-a)+b2(c+a-b)+c2(a+b-c)≤ba(b+c-a)+cb(c+a-b)+ac(a+b-c),①
及a2(b+c-a)+b2(c+a-b)+c2(a+b-c)≤ca(b+c-a)+ab(c+a-b)+bc(a+b-c),②
①+②并化简即得a2(b+c-a)+b2(c+a-b)+c2(a+b-c)≤3abc.
点评 本题考查排序不等式的应用,不等式的证明,考查逻辑推理能力.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
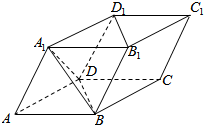 如图,四棱柱ABCD-A1B1C1D1中,所有棱长均为a,且∠A1AB=∠A1AD=∠DAB=60°,则下列结论正确的是①②④⑤(写出所有正确的结论的编号).
如图,四棱柱ABCD-A1B1C1D1中,所有棱长均为a,且∠A1AB=∠A1AD=∠DAB=60°,则下列结论正确的是①②④⑤(写出所有正确的结论的编号).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图正方体ABCD-A1B1C1D1中,下列结论中正确的序号是①③.
如图正方体ABCD-A1B1C1D1中,下列结论中正确的序号是①③.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为梯形,BC∥AD,AB⊥AD,PA=AB=BC=1,AD=2.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为梯形,BC∥AD,AB⊥AD,PA=AB=BC=1,AD=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 方程 | 根的个数 | 方程 | 根的个数 |
| f(x)-5=0 | 1 | f(x)+4=0 | 3 |
| f(x)-3=0 | 3 | f(x)+6=0 | 1 |
| f(x)=0 | 3 |
| A. | -6<a<-4 | B. | -4<a<0 | C. | 0<a<3 | D. | 3<a<5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com