
ЁОЬтФПЁПдк![]() ФъГѕЕФЪБКђЃЌЙњМвеўИЎЙЄзїБЈИцУїШЗЬсГіЃЌ
ФъГѕЕФЪБКђЃЌЙњМвеўИЎЙЄзїБЈИцУїШЗЬсГіЃЌ ![]() ФъвЊМсОіДђКУРЖЬьБЃЮРеНЃЌМгПьНтОіШМУКЮлШОЮЪЬтЃЌШЋУцЪЕЪЉЩЂУКзлКЯжЮРэ.ЪЕЪЉУКИФЕчЙЄГЬКѓЃЌФГЯиГЧЕФНќСљИідТЕФдТгУУКСПж№НЅМѕЩйЃЌ
ФъвЊМсОіДђКУРЖЬьБЃЮРеНЃЌМгПьНтОіШМУКЮлШОЮЪЬтЃЌШЋУцЪЕЪЉЩЂУКзлКЯжЮРэ.ЪЕЪЉУКИФЕчЙЄГЬКѓЃЌФГЯиГЧЕФНќСљИідТЕФдТгУУКСПж№НЅМѕЩйЃЌ ![]() дТжС
дТжС![]() дТЕФгУУКСПШчЯТБэЫљЪОЃК
дТЕФгУУКСПШчЯТБэЫљЪОЃК
дТЗн |
|
|
|
|
|
|
гУУКСП |
|
|
|
|
|
|
ЃЈ1ЃЉгЩгкФГаЉдвђЃЌ ![]() жавЛИіЪ§ОнЖЊЪЇЃЌЕЋИљОн
жавЛИіЪ§ОнЖЊЪЇЃЌЕЋИљОн![]() жС
жС![]() дТЗнЕФЪ§ОнЕУГі
дТЗнЕФЪ§ОнЕУГі![]() бљБОЦНОљжЕЪЧ
бљБОЦНОљжЕЪЧ![]() ЃЌЧѓГіЖЊЪЇЕФЪ§ОнЃЛ
ЃЌЧѓГіЖЊЪЇЕФЪ§ОнЃЛ
ЃЈ2ЃЉЧыИљОн![]() жС
жС![]() дТЗнЕФЪ§ОнЃЌЧѓГі
дТЗнЕФЪ§ОнЃЌЧѓГі![]() Йигк
Йигк![]() ЕФЯпадЛиЙщЗНГЬ
ЕФЯпадЛиЙщЗНГЬ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЯждкгУЃЈ2ЃЉжаЕУЕНЕФЯпадЛиЙщЗНГЬжаЕУЕНЕФЙРМЦЪ§Онгы![]() дТ
дТ![]() дТЕФЪЕМЪЪ§ОнЕФЮѓВюРДХаЖЯИУЕиЧјЕФИФдьЯюФПЪЧЗёДяЕНдЄЦкЃЌШєЮѓВюОљВЛГЌЙ§
дТЕФЪЕМЪЪ§ОнЕФЮѓВюРДХаЖЯИУЕиЧјЕФИФдьЯюФПЪЧЗёДяЕНдЄЦкЃЌШєЮѓВюОљВЛГЌЙ§![]() ЃЌдђШЯЮЊИУЕиЧјЕФИФдьвбОДяЕНдЄЦкЃЌЗёдђШЯЮЊИФдьЮДДядЄЦкЃЌЧыХаЖЯИУЕиЧјЕФУКИФЕчЯюФПЪЧЗёДядЄЦкЃП
ЃЌдђШЯЮЊИУЕиЧјЕФИФдьвбОДяЕНдЄЦкЃЌЗёдђШЯЮЊИФдьЮДДядЄЦкЃЌЧыХаЖЯИУЕиЧјЕФУКИФЕчЯюФПЪЧЗёДядЄЦкЃП
ЃЈВЮПМЙЋЪНЃКЯпадЛиЙщЗНГЬ![]() ЃЌЦфжа
ЃЌЦфжа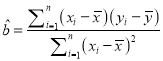
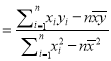 ЃЉ
ЃЉ
ЁОД№АИЁПЃЈ1ЃЉ4ЃЈ2ЃЉ![]() ЃЈ3ЃЉИУЕиЧјЕФУКИФЕчЯюФПвбОДяЕНдЄЦк
ЃЈ3ЃЉИУЕиЧјЕФУКИФЕчЯюФПвбОДяЕНдЄЦк
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнЦНОљЪ§МЦЫуЙЋЪНЕУ![]() ЃЌНтЕУЖЊЪЇЕФЪ§ОнЃЛЃЈ2ЃЉИљОнЙЋЪНЧѓ
ЃЌНтЕУЖЊЪЇЕФЪ§ОнЃЛЃЈ2ЃЉИљОнЙЋЪНЧѓ![]() ЃЌдйИљОн
ЃЌдйИљОн![]() Чѓ
Чѓ![]() ЃЛЃЈ3ЃЉИљОнЯпадЛиЙщЗНГЬЧѓЙРМЦЪ§ОнЃЌВЂгыЪЕМЪЪ§ОнБШНЯЮѓВюЃЌШЗЖЈНсТл.
ЃЛЃЈ3ЃЉИљОнЯпадЛиЙщЗНГЬЧѓЙРМЦЪ§ОнЃЌВЂгыЪЕМЪЪ§ОнБШНЯЮѓВюЃЌШЗЖЈНсТл.
ЪдЬтНтЮіЃКНтЃКЃЈ1ЃЉЩшЖЊЪЇЕФЪ§ОнЮЊ![]() ЃЌдђ
ЃЌдђ![]()
ЕУ![]() ЃЌМДЖЊЪЇЕФЪ§ОнЪЧ
ЃЌМДЖЊЪЇЕФЪ§ОнЪЧ![]() .
.
ЃЈ2ЃЉгЩЪ§ОнЧѓЕУ![]() ЃЌ
ЃЌ
гЩЙЋЪНЧѓЕУ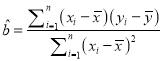
![]()
![]()
Ыљвд![]() Йигк
Йигк![]() ЕФЯпадЛиЙщЗНГЬЮЊ
ЕФЯпадЛиЙщЗНГЬЮЊ![]()
ЃЈ3ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() ЃЌ
ЃЌ ![]()
ЭЌбљЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() ЃЌ
ЃЌ ![]()
ЫљвдЃЌИУЕиЧјЕФУКИФЕчЯюФПвбОДяЕНдЄЦк


 аЧМЖПкЫуЬьЬьСЗЯЕСаД№АИ
аЧМЖПкЫуЬьЬьСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩш![]() ЮЊЦцКЏЪ§ЃЌ
ЮЊЦцКЏЪ§ЃЌ![]() ЮЊЪЕГЃЪ§ЃЎ
ЮЊЪЕГЃЪ§ЃЎ
ЃЈ1ЃЉЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉжЄУїЃК![]() дкЧјМф
дкЧјМф![]() ФкЕЅЕїЕндіЃЛ
ФкЕЅЕїЕндіЃЛ
ЃЈ3ЃЉШєЖдгкЧјМф![]() ЩЯЕФУПвЛИі
ЩЯЕФУПвЛИі![]() ЕФжЕЃЌВЛЕШЪН
ЕФжЕЃЌВЛЕШЪН![]() КуГЩСЂЃЌЧѓЪЕЪ§
КуГЩСЂЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФЖўДЮКЏЪ§fЃЈxЃЉ=ax2Љ4bx+1ЃЎЩшМЏКЯP={1ЃЌ2ЃЌ3}КЭQ={Љ1ЃЌ1ЃЌ2ЃЌ3ЃЌ4}ЃЌЗжБ№ДгМЏКЯPКЭQжаЫцЛњШЁвЛИіЪ§зїЮЊaКЭbЃЌЧѓКЏЪ§y=fЃЈxЃЉдкЧјМф[1ЃЌ+ЁоЃЉЩЯЪЧдіКЏЪ§ЕФИХТЪ
ЃЈ1ЃЉвбжЊЙигкxЕФЖўДЮКЏЪ§fЃЈxЃЉ=ax2Љ4bx+1ЃЎЩшМЏКЯP={1ЃЌ2ЃЌ3}КЭQ={Љ1ЃЌ1ЃЌ2ЃЌ3ЃЌ4}ЃЌЗжБ№ДгМЏКЯPКЭQжаЫцЛњШЁвЛИіЪ§зїЮЊaКЭbЃЌЧѓКЏЪ§y=fЃЈxЃЉдкЧјМф[1ЃЌ+ЁоЃЉЩЯЪЧдіКЏЪ§ЕФИХТЪЃЛ
ЃЈ2ЃЉдкЧјМф[1ЃЌ5]КЭ[2ЃЌ4]ЩЯЗжБ№ШЁвЛИіЪ§ЃЌМЧЮЊaЃЌbЃЌЧѓЗНГЬ ![]() +
+ ![]() =1БэЪОНЙЕудкxжсЩЯЧвРыаФТЪаЁгк
=1БэЪОНЙЕудкxжсЩЯЧвРыаФТЪаЁгк ![]() ЕФЭждВЕФИХТЪЃЎ
ЕФЭждВЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГГЕМфЕФвЛЬЈЛњДВЩњВњГівЛХњСуМўЃЌЯжДгжаГщШЁ8МўЃЌНЋЦфБрЮЊ![]() ЃЌ
ЃЌ ![]() ЃЌЁЃЌ
ЃЌЁЃЌ ![]() ЃЌВтСПЦфГЄЖШЃЈЕЅЮЛЃК
ЃЌВтСПЦфГЄЖШЃЈЕЅЮЛЃК ![]() ЃЉЃЌЕУЕНЯТБэжаЪ§ОнЃК
ЃЉЃЌЕУЕНЯТБэжаЪ§ОнЃК
БрКХ |
|
|
|
|
|
|
|
|
ГЄЖШ | 1.49 | 1.46 | 1.51 | 1.51 | 1.53 | 1.51 | 1.47 | 1.51 |
ЦфжаГЄЖШдкЧјМф![]() ФкЕФСуМўЮЊвЛЕШЦЗ.
ФкЕФСуМўЮЊвЛЕШЦЗ.
ЃЈ1ЃЉДгЩЯЪі8ИіСуМўжаЃЌЫцЛњГщШЁвЛИіЃЌЧѓетИіСуМўЮЊвЛЕШЦЗЕФИХТЪЃЛ
ЃЈ2ЃЉДгвЛЕШЦЗСуМўжаЃЌЫцЛњГщШЁ2Иі.
ЂйгУСуМўЕФБрКХСаГіЫљгаПЩФмЕФГщШЁНсЙћЃЛ
ЂкЧѓет2ИіСуМўГЄЖШЯрЕШЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫФИіКЏЪ§жаЃЌвдІаЮЊзюаЁе§жмЦкЃЌЧвдкЧјМф ![]() ЩЯЮЊМѕКЏЪ§ЕФЪЧЃЈЁЁЁЁЃЉ
ЩЯЮЊМѕКЏЪ§ЕФЪЧЃЈЁЁЁЁЃЉ
A.y=2|sinx|
B.y=cosx
C.y=sin2x
D.y=|cosx|
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=sin2xЉ ![]() sinxcosx+
sinxcosx+ ![]() ЃЌgЃЈxЃЉ=mcosЃЈx+
ЃЌgЃЈxЃЉ=mcosЃЈx+ ![]() ЃЉЉm+2
ЃЉЉm+2
ЃЈ1ЃЉШєЖдШЮвтЕФx1 ЃЌ x2ЁЪ[0ЃЌІа]ЃЌОљгаfЃЈx1ЃЉЁнgЃЈx2ЃЉЃЌЧѓmЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉШєЖдШЮвтЕФxЁЪ[0ЃЌІа]ЃЌОљгаfЃЈxЃЉЁнgЃЈxЃЉЃЌЧѓmЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшaЃЌbЁЪRЃЌcЁЪ[0ЃЌ2ІаЃЉЃЌШєЖдгкШЮвтЪЕЪ§xЖМга2sinЃЈ3xЉ ![]() ЃЉ=asinЃЈbx+cЃЉЃЌдђТњзуЬѕМўЕФгаађЪЕЪ§зщЃЈaЃЌbЃЌcЃЉЕФзщЪ§ЮЊ ЃЎ
ЃЉ=asinЃЈbx+cЃЉЃЌдђТњзуЬѕМўЕФгаађЪЕЪ§зщЃЈaЃЌbЃЌcЃЉЕФзщЪ§ЮЊ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГбаОПЫљМЦЛЎРћгУЁАЩёЪЎЁБгюжцЗЩДЌНјаааТВњЦЗДюдиЪЕбщЃЌМЦЛЎДюдиШєИЩМўаТВњЦЗAЁЂBЃЌИУЫљвЊИљОнИУВњЦЗЕФбажЦГЩБОЁЂВњЦЗжиСПЁЂДюдиЪЕбщЗбгУКЭдЄМЦВњЩњЕФЪевцРДОіЖЈОпЬхДюдиАВХХЃЌгаЙиЪ§ОнШчБэЃК
УПМўВњЦЗA | УПМўВњЦЗB | ||
бажЦГЩБОЁЂДюди | 20 | 30 | МЦЛЎзюДѓзЪН№Жю |
ВњЦЗжиСПЃЈЧЇПЫЃЉ | 10 | 5 | зюДѓДюдижиСП110ЧЇПЫ |
дЄМЦЪевцЃЈЭђдЊЃЉ | 80 | 60 |
ЗжБ№гУxЃЌyБэЪОДюдиаТВњЦЗAЃЌBЕФМўЪ§ЃЎзмЪевцгУZБэЪО
ЃЈЂёЃЉгУxЃЌyСаГіТњзуЩњВњЬѕМўЕФЪ§бЇЙиЯЕЪНЃЌВЂЛГіЯргІЕФЦНУцЧјгђЃЛ
ЃЈЂђЃЉЮЪЗжБ№ДюдиаТВњЦЗAЁЂBИїЖрЩйМўЃЌВХФмЪЙзмдЄМЦЪевцДяЕНзюДѓЃПВЂЧѓГіДЫзюДѓЪевцЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкГЄЗНЬхABCDЉA1B1C1D1жаЃЌA1C1гыB1D1ЕФНЛЕуЮЊO1 ЃЌ ACгыBDЕФНЛЕуЮЊOЃЎ
ЃЈ1ЃЉЧѓжЄЃКжБЯпOO1ЁЮЦНУцBCC1B1ЃЛ
ЃЈ2ЃЉШєAB=BCЃЌЧѓжЄЃКжБЯпBOЁЭЦНУцACC1A1 ЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com