
【题目】如图,在正方体ABCD – A1B1C1D1中,点E,F,G分别是棱BC,A1B1,B1C1的中点.
(1)求异面直线EF与DG所成角的余弦值;
(2)设二面角A—BD—G的大小为θ,求 |cosθ| 的值.

【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:(1)建立空间直角坐标系,进而通过计算 即可得解;
即可得解;
(2)计算得平面DBG和平面ABD的法向量n1和n2,通过计算cos<n1,n2>即可得解.
试题解析:
如图,以{![]() ,
,![]() ,
,![]() }为正交基底建立坐标系D—xyz.
}为正交基底建立坐标系D—xyz.

设正方体的边长为2,则D(0,0,0),A(2,0,0),
B(2,2,0),E(1,2,0),F(2,1,2),G(1,2,2).
(1)因为![]() =(2,1,2)-(1,2,0)=(1,-1,2),
=(2,1,2)-(1,2,0)=(1,-1,2),
![]() = (1,2,2),
= (1,2,2),
所以![]() ·
·![]() =1×1+(-1)×2+2×2=3,
=1×1+(-1)×2+2×2=3,
|![]() |=
|=![]() =
=![]() ,|
,|![]() |=3.
|=3.
从而cos<![]() ,
,![]() >=
>=![]() =
=![]() =
=![]() ,
,
即向量![]() 与
与![]() 的夹角的余弦为
的夹角的余弦为![]() ,
,
从而异面直线EF与DG所成角的余弦值为![]() .
.
(2)![]() =(2,2,0),
=(2,2,0),![]() = (1,2,2).
= (1,2,2).
设平面DBG的一个法向量为n1=(x,y,z ).
由题意,得 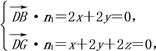
取x=2,可得y=-2,z=1.
所以n1=(2,-2,1).
又平面ABD的一个法向量n2=![]() =(0,0,2),
=(0,0,2),
所以cos<n1,n2>=![]() =
=![]() =
=![]() .
.
因此 |cosθ|=![]() .
.


科目:高中数学 来源: 题型:
【题目】给定集合A={a1 , a2 , a3 , …,an}(n∈N* , n≥3)中,定义ai+aj(1≤i<j≤n,i,j∈N*)中所有不同值的个数为集合A两元素和的容量,用L(A)表示.若数列{an}是公差不为0的等差数列,设集合A={a1 , a2 , a3 , …,a2016},则L(A)= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cos2ωx+ ![]() sin2ωx(ω>0)的最小正周期为π,给出下列四个命题:
sin2ωx(ω>0)的最小正周期为π,给出下列四个命题:
①f(x)的最大值为3;
②将f(x)的图象向左平移 ![]() 后所得的函数是偶函数;
后所得的函数是偶函数;
③f(x)在区间[﹣ ![]() ,
, ![]() ]上单调递增;
]上单调递增;
④f(x)的图象关于直线x= ![]() 对称.
对称.
其中正确说法的序号是( )
A.②③
B.①④
C.①②④
D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域为R,并且图象关于y轴对称,当x≤-1时,y=f(x)的图象是经过点(-2,0)与(-1,1)的射线,又在y=f(x)的图象中有一部分是顶点在(0,2),且经过点(1,1)的一段抛物线.
(1)试求出函数f(x)的表达式,作出其图象;
(2)根据图象说出函数的单调区间,以及在每一个单调区间上函数是增函数还是减函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直角坐标系xOy中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ2﹣4ρsinθ+3=0,A、B两点极坐标分别为(1,π)、(1,0).
(1)求曲线C的参数方程;
(2)在曲线C上取一点P,求|AP|2+|BP|2的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=![]() ax2-1-lnx,其中a∈R.
ax2-1-lnx,其中a∈R.
(1)若a=0,求过点(0,-1)且与曲线y=f(x)相切的直线方程;
(2)若函数f(x)有两个零点x1,x2,
① 求a的取值范围;
② 求证:f ′(x1)+f ′(x2)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:y=﹣x+1与椭圆C: ![]() =1(a>b>0))相交于不同的两点A、B,且线段AB的中点P的坐标为(
=1(a>b>0))相交于不同的两点A、B,且线段AB的中点P的坐标为( ![]() ,
, ![]() )
) 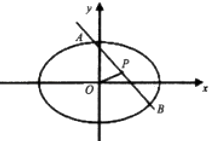
(1)求椭圆C离心率;
(2)设O为坐标原点,且2|OP|=|AB|,求椭圆C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关命题的说法中错误的是
A. 在频率分布直方图中,中位数左边和右边的直方图的面积相等 .
B. 一个样本的方差是![]() ,则这组数据的总和等于60.
,则这组数据的总和等于60.
C. 在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越差.
D. 对于命题![]() 使得
使得![]() <0,则
<0,则![]() ,使
,使![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com