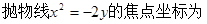
。
试题分析:根据抛物线性质可知其焦点为
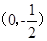
.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
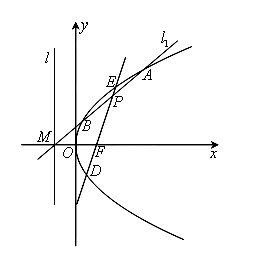
如图,设抛物线
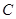
:
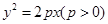
的焦点为
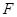
,准线为
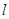
,过准线
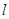
上一点
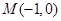
且斜率为
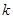
的直线
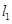
交抛物线
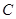
于
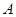
,
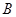
两点,线段
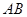
的中点为
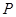
,直线
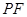
交抛物线
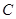
于
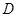
,
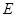
两点.
(1)求抛物线
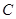
的方程及
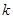
的取值范围;
(2)是否存在
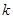
值,使点
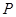
是线段
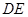
的中点?若存在,求出
值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
已知直线
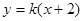
(k>0)与抛物线
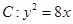
相交于
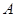
、
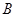
两点,
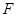
为
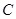
的焦点,若
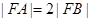
,则k的值为
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
准线方程为x=3的抛物线的标准方程为 ( )
| A.y2=-6x | B.y2=6x |
| C.y2=-12x | D.y2="12x" |
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
直线
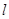
过抛物线

的焦点,且交抛物线于
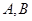
两点,交其准线于
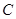
点,已知

,则
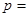
( )
| A.2 | B.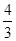 | C. | D.4 |
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知
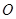
为坐标原点,
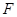
为抛物线
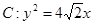
的焦点,
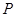
为
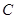
上一点,若
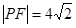
,则△
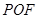
的面积为( )
| A.2 | B.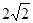 | C.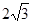 | D.4 |
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知抛物线方程为
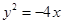
,则它的焦点坐标为( )
查看答案和解析>>

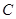 :
: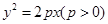 的焦点为
的焦点为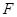 ,准线为
,准线为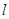 ,过准线
,过准线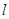 上一点
上一点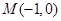 且斜率为
且斜率为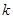 的直线
的直线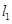 交抛物线
交抛物线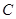 于
于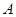 ,
,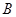 两点,线段
两点,线段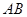 的中点为
的中点为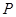 ,直线
,直线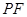 交抛物线
交抛物线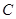 于
于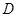 ,
,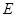 两点.
两点. 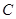 的方程及
的方程及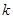 的取值范围;
的取值范围;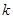 值,使点
值,使点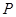 是线段
是线段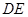 的中点?若存在,求出
的中点?若存在,求出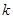 值,若不存在,请说明理由.
值,若不存在,请说明理由. 