
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)若函数![]() 在
在![]() 处取得极大值,求实数
处取得极大值,求实数![]() 的值
的值
(2)函数![]() ,当
,当![]() 时,
时,![]() 在
在![]() 处取得最大值,求实数
处取得最大值,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由题意得出![]() ,可求得实数
,可求得实数![]() 的值,然后将实数
的值,然后将实数![]() 的值代入导数,就函数
的值代入导数,就函数![]() 是否在
是否在![]() 处极大值进行检验,由此可得出实数
处极大值进行检验,由此可得出实数![]() 的值;
的值;
(2)求得![]() 以及
以及![]() ,对实数
,对实数![]() 分
分![]() 、
、![]() 、
、![]() 三种情况讨论,利用导数分析函数
三种情况讨论,利用导数分析函数![]() 在区间
在区间![]() 的单调性,结合函数
的单调性,结合函数![]() 在
在![]() 处取得最值进行验证或得出不等式,进而可求得实数
处取得最值进行验证或得出不等式,进而可求得实数![]() 的取值范围.
的取值范围.
(1)![]() ,
,![]() ,
,
由题意可得![]() ,整理得
,整理得![]() ,解得
,解得![]() 或
或![]() .
.
当![]() 时,
时,![]() 恒成立,
恒成立,
此时,函数![]() 在
在![]() 上单调递增,无极值;
上单调递增,无极值;
当![]() 时,
时,![]() .
.
令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() 或
或![]() .
.
此时,函数![]() 在
在![]() 处取得极大值,合乎题意.
处取得极大值,合乎题意.
综上所述,![]() ;
;
(2)![]() ,
,
![]() .
.
①当![]() 时,
时,![]() 对任意的
对任意的![]() 恒成立,
恒成立,
此时,函数![]() 单调递减,
单调递减,![]() ,合乎题意;
,合乎题意;
②当![]() 时,对于函数
时,对于函数![]() ,
,![]() 恒成立,
恒成立,
设方程![]() 的两根分别为
的两根分别为![]() 、
、![]() ,则
,则![]() ,设
,设![]() ,则
,则![]() .
.
(i)若![]() ,则当
,则当![]() 时,
时,![]() ,此时函数
,此时函数![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,此时函数
,此时函数![]() 单调递增.
单调递增.
所以,![]() ,则
,则![]() ,即
,即![]() ,解得
,解得![]() ,
,
此时![]() ,解得
,解得![]() ,则
,则![]() ;
;
(ii)当![]() 时,即
时,即![]() ,得
,得![]() ,
,
则![]() 对任意的
对任意的![]() 恒成立,此时,函数
恒成立,此时,函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
则![]() ,合乎题意;
,合乎题意;
③当![]() 时,对任意的
时,对任意的![]() ,
,![]() ,此时,函数
,此时,函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
则![]() ,合乎题意.
,合乎题意.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】在传染病学中,通常把从致病刺激物侵入机体或者对机体发生作用起,到机体出现反应或开始呈现该疾病对应的相关症状时止的这一阶段称为潜伏期.一研究团队统计了某地区100名患者的相关信息,得到如下表格:
潜伏期(单位:天) |
|
|
|
|
|
|
|
人数 | 85 | 205 | 310 | 250 | 130 | 15 | 5 |
(1)求这1000名患者的潜伏期的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)该传染病的潜伏期受诸多因素的影响,为研究潜伏期与患者年龄的关系,以潜伏期是否超过6天为标准进行分层抽样,从上述1000名患者中抽取200人,得到如下列联表.请将列联表补充完整,并根据列联表判断是否有95%的把握认为潜伏期与患者年龄有关;
潜伏期 | 潜伏期 | 总计 | |
50岁以上(含50岁) | 100 | ||
50岁以下 | 55 | ||
总计 | 200 |
附:
| 0.05 | 0.025 | 0.010 |
| 3.841 | 5.024 | 6.635 |
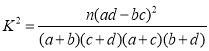 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 为抛物线
为抛物线![]() 上一点,斜率分别为
上一点,斜率分别为![]() ,
,![]()
![]() 的直线PA,PB分别交抛物线于点A,B(不与点P重合).
的直线PA,PB分别交抛物线于点A,B(不与点P重合).

(1)证明:直线AB的斜率为定值;
(2)若△ABP的内切圆半径为![]() .
.
(i)求△ABP的周长(用k表示);
(ii)求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国唐代天文学家、数学家张逐曾以“李白喝酒”为题编写了如下一道题:“李白街上走,提壶去买酒,遇店加一倍,见花喝一斗(计量单位),三遇店和花,喝光壶中酒.”问最后一次遇花时有酒________斗,原有酒________斗.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三校柱![]() 中,
中,![]() 是等直角三角形,
是等直角三角形,![]() ,
,![]() ,M是AB的中点,且
,M是AB的中点,且![]() .
.
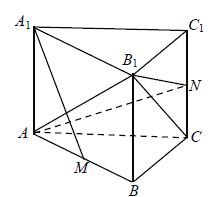
(1)求![]() 的长;
的长;
(2)已知点N在棱![]() 上,若平面
上,若平面![]() 与平面
与平面![]() 所成锐二面角的平面角的余弦值为
所成锐二面角的平面角的余弦值为![]() ,试确定点N的位置.
,试确定点N的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
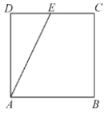
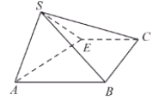
【题目】如图,点![]() 为正方形
为正方形![]() 边
边![]() 上异于点
上异于点![]() ,
,![]() 的动点,将
的动点,将![]() 沿
沿![]() 翻折成
翻折成![]() ,在翻折过程中,下列说法正确的是( )
,在翻折过程中,下列说法正确的是( )
A.存在点![]() 和某一翻折位置,使得
和某一翻折位置,使得![]()
B.存在点![]() 和某一翻折位置,使得
和某一翻折位置,使得![]() 平面
平面![]()
C.存在点![]() 和某一翻折位置,使得直线
和某一翻折位置,使得直线![]() 与平面
与平面![]() 所成的角为45°
所成的角为45°
D.存在点![]() 和某一翻折位置,使得二面角
和某一翻折位置,使得二面角![]() 的大小为60°
的大小为60°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某总公司在A,B两地分别有甲、乙两个下属公司同种新能源产品(这两个公司每天都固定生产50件产品),所生产的产品均在本地销售.产品进人市场之前需要对产品进行性能检测,得分低于80分的定为次品,需要返厂再加工;得分不低于80分的定为正品,可以进人市场.检测员统计了甲、乙两个下属公司100天的生产情况及每件产品盈利亏损情况,数据如表所示:
表1
甲公司 | 得分 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
件数 | 10 | 10 | 40 | 40 | 50 | |
天数 | 10 | 10 | 10 | 10 | 80 |
表2
甲公司 | 得分 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
件数 | 10 | 5 | 40 | 45 | 50 | |
天数 | 20 | 10 | 20 | 10 | 70 |
表3
每件正品 | 每件次品 | |
甲公司 | 盈2万元 | 亏3万元 |
乙公司 | 盈3万元 | 亏3.5万元 |
(1)分别求甲、乙两个公司这100天生产的产品的正品率(用百分数表示).
(2)试问甲、乙两个公司这100天生产的产品的总利润哪个更大?说明理由.
(3)若以甲公司这100天中每天产品利润总和对应的频率作为概率,从甲公司这100天随机抽取1天,记这天产品利润总和为X,求X的分布列及其数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com