
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是直角梯形,侧棱
是直角梯形,侧棱![]() 底面
底面![]() ,
,![]() 垂直于
垂直于![]() 和
和![]() ,
,![]() 为棱
为棱![]() 上的点,
上的点,![]() ,
,![]() .
.
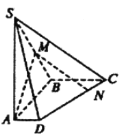
(1)若![]() 为棱
为棱![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)当![]() 时,求平面
时,求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;
(3)在第(2)问条件下,设点![]() 是线段
是线段![]() 上的动点,
上的动点,![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求当
,求当![]() 取最大值时点
取最大值时点![]() 的位置.
的位置.
【答案】(1)证明见解析;(2)![]() ;(3)当
;(3)当![]() 最大时,点N在线段CD上,且
最大时,点N在线段CD上,且![]() .
.
【解析】
(1)取线段SC的中点E,根据中位线定理即可证明![]() ,因而得到AMED为平行四边形,即可证明
,因而得到AMED为平行四边形,即可证明![]() 平面SCD.
平面SCD.
(2)建立空间直角坐标系,写出各个点的坐标,因而可以求得平面AMC和平面SAB的法向量,利用法向量的数量积求得平面AMC与平面SAB所成的锐二面角的余弦值即可。
(3)设出N点坐标,利用直线与平面夹角的正弦值即为直线与平面法向量夹角的余弦值即可求得![]() 的表达式;根据基本不等式成立的条件,求得N点的坐标,即可判断出N点的位置。
的表达式;根据基本不等式成立的条件,求得N点的坐标,即可判断出N点的位置。
(1)证明:取线段SC的中点E,连接ME,ED.
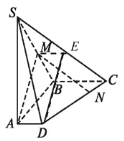
在![]() 中,ME为中位线,∴
中,ME为中位线,∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴四边形AMED为平行四边形.
∴![]() .
.
∵![]() 平面SCD,
平面SCD,![]() 平面SCD,
平面SCD,
∴![]() 平面SCD.
平面SCD.
(2)解:以点A为坐标原点,建立分别以AD、AB、AS为x轴、y轴、z轴,如图所示的空间直角坐标系,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由条件得M为线段SB近B点的三等分点.
于是![]() ,即
,即![]()
设平面AMC的一个法向量为![]() ,则
,则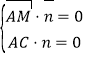 ,
,
将坐标代入得![]() ,
,
另外易知平面SAB的一个法向量为![]() ,
,
所以平面AMC与平面SAB所成的锐二面角的余弦为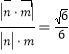 .
.
(3)设![]() ,其中
,其中![]() .
.
由于![]() ,所以
,所以![]() .
.
所以 ,
,
可知当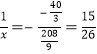 ,即
,即![]() 时分母有最小值,此时
时分母有最小值,此时![]() 有最大值,
有最大值,
此时,![]() ,即点N在线段CD上且
,即点N在线段CD上且![]() .
.


科目:高中数学 来源: 题型:
【题目】数学中有许多形状优美、寓意美好的曲线,曲线C:![]() 就是其中之一(如图).给出下列三个结论:
就是其中之一(如图).给出下列三个结论:
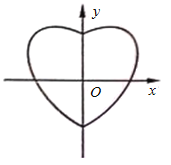
①曲线C恰好经过6个整点(即横、纵坐标均为整数的点);
②曲线C上任意一点到原点的距离都不超过![]() ;
;
③曲线C所围成的“心形”区域的面积小于3.
其中,所有正确结论的序号是
A. ①B. ②C. ①②D. ①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用0与1两个数字随机填入如图所示的5个格子里,每个格子填一个数字,并且从左到右数,不管数到哪个格子,总是1的个数不少于0的个数,则这样填法的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有四座城市![]() 、
、![]() 、
、![]() 、
、![]() ,其中
,其中![]() 在
在![]() 的正东方向,且与
的正东方向,且与![]() 相距
相距![]() ,
,![]() 在
在![]() 的北偏东
的北偏东![]() 方向,且与
方向,且与![]() 相距
相距![]() ;
;![]() 在
在![]() 的北偏东
的北偏东![]() 方向,且与
方向,且与![]() 相距
相距![]() ,一架飞机从城市
,一架飞机从城市![]() 出发以
出发以![]() 的速度向城市
的速度向城市![]() 飞行,飞行了
飞行,飞行了![]() ,接到命令改变航向,飞向城市
,接到命令改变航向,飞向城市![]() ,此时飞机距离城市
,此时飞机距离城市![]() 有( )
有( )
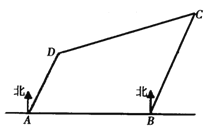
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下面几种说法:
①相等向量的坐标相同;
②若向量![]() 满足
满足![]() ,则
,则![]()
③若![]() ,
,![]() ,
,![]() ,
,![]() 是不共线的四点,则“
是不共线的四点,则“![]() ”是“四边形
”是“四边形![]() 为平行四边形”的充要条件;
为平行四边形”的充要条件;
④![]() 的充要条件是
的充要条件是![]() 且
且![]() .
.
其中正确说法的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有限集合S中元素的个数记做![]() ,设A,B都为有限集合,给出下列命题:
,设A,B都为有限集合,给出下列命题:
①![]() 的充要条件是
的充要条件是![]()
②![]() 的必要不充分条件是
的必要不充分条件是![]()
③![]() 的充分不必要条件是
的充分不必要条件是![]()
④![]() 的充要条件是
的充要条件是![]()
其中,真命题有( )
A.①②③B.①②C.②③D.①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com