
【题目】在数列{an}中, ![]() ,an+1=
,an+1= ![]() .
.
(1)计算a2 , a3 , a4并猜想数列{an}的通项公式;
(2)用数学归纳法证明你的猜想.
【答案】
(1)解:∵ ![]() ,an+1=
,an+1= ![]() .
.
∴a2= ![]() =
= ![]() ,a3=
,a3= ![]() =
= ![]() ,a4=
,a4= ![]() =
= ![]()
猜想数列{an}的通项公式为an= ![]()
(2)解:①n=1时,a1= ![]() =
= ![]() 满足通项公式;
满足通项公式;
②假设当n=k时猜想成立,即 ![]() ,则
,则 ![]() =
= ![]() =
= ![]() ,
,
当n=k+1时猜想也成立.
综合①②,对n∈N*猜想都成立
【解析】(1)根据 ![]() ,an+1=
,an+1= ![]() 可求出a2 , a3 , a4的值,根据前四项的值可猜想数列{an}的通项公式;(2)根据数学归纳法的步骤进行证明即可.
可求出a2 , a3 , a4的值,根据前四项的值可猜想数列{an}的通项公式;(2)根据数学归纳法的步骤进行证明即可.
【考点精析】利用数列的通项公式和数学归纳法的定义对题目进行判断即可得到答案,需要熟知如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式;数学归纳法是证明关于正整数n的命题的一种方法.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:高中数学 来源: 题型:
【题目】已知不等式x2+mx+3≤0的解集为A=[1,n],集合B={x|x2﹣ax+a≤0}.
(1)求m﹣n的值;
(2)若A∪B=A,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)= ![]() +lg(x﹣1)+(x﹣3)0 的定义域为( )
+lg(x﹣1)+(x﹣3)0 的定义域为( )
A.{x|1<x≤4}
B.{x|1<x≤4且x≠3}
C.{x|1≤x≤4且x≠3}
D.{x|x≥4}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体ABCD﹣A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点. 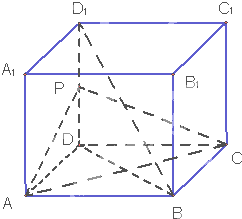
(1)求证:直线BD1∥平面PAC;
(2)求证:平面PAC⊥平面BDD1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在[﹣1,1]上的奇函数,且f(1)=1,若m,n∈[﹣1,1],m+n≠0时,有 ![]() >0.
>0.
(Ⅰ)证明f(x)在[﹣1,1]上是增函数;
(Ⅱ)解不等式f(x2﹣1)+f(3﹣3x)<0
(Ⅲ)若f(x)≤t2﹣2at+1对x∈[﹣1,1],a∈[﹣1,1]恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用M[A]表示非空集合A中的元素个数,记|A﹣B|= ![]() ,若A={1,2,3},B={x||x2﹣2x﹣3|=a},且|A﹣B|=1,则实数a的取值范围为 .
,若A={1,2,3},B={x||x2﹣2x﹣3|=a},且|A﹣B|=1,则实数a的取值范围为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】集合A={(x,y)|y=a|x|,x∈R},B={(x,y)|y=x+a,x∈R},已知集合A∩B中有且仅有一个元素,则常数a的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com