
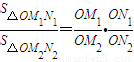 .若从点O所作的不在同一个平面内的三条射线OP,OQ和OR上分别有点P1,P2与点Q1,Q2和R1,R2,则类似的结论为: .
.若从点O所作的不在同一个平面内的三条射线OP,OQ和OR上分别有点P1,P2与点Q1,Q2和R1,R2,则类似的结论为: . 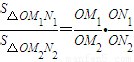 .(面的性质)我们可以类比在空间中相似的体的性质.
.(面的性质)我们可以类比在空间中相似的体的性质.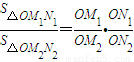 .
.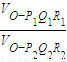 =
=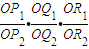
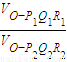 =
=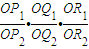


科目:高中数学 来源: 题型:
| S△OM1N1 |
| S△OM2N2 |
| OM1 |
| OM2 |
| ON1 |
| ON2 |
查看答案和解析>>
科目:高中数学 来源:全优设计选修数学-2-2苏教版 苏教版 题型:022
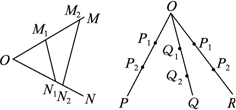
(经典回放)如图所示,若从点O所作的两条射线OM、ON上分别有点M1、M2与点N1、N2,则三角形面积之比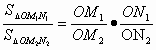 .若从点O所作的不在同一平面内的三条射线OP、OQ和OR上,分别有点P1、P2,点Q1、Q2和点R1、R2,则类似的结论为_________.
.若从点O所作的不在同一平面内的三条射线OP、OQ和OR上,分别有点P1、P2,点Q1、Q2和点R1、R2,则类似的结论为_________.
查看答案和解析>>
科目:高中数学 来源:2008-2009学年福建省厦门六中高三(上)期中数学模拟试卷1(理科)(解析版) 题型:填空题
 .若从点O所作的不在同一个平面内的三条射线OP,OQ和OR上分别有点P1,P2与点Q1,Q2和R1,R2,则类似的结论为: .
.若从点O所作的不在同一个平面内的三条射线OP,OQ和OR上分别有点P1,P2与点Q1,Q2和R1,R2,则类似的结论为: .查看答案和解析>>
科目:高中数学 来源:2009-2010学年数学寒假作业(02)(解析版) 题型:填空题
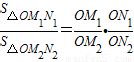 .若从点O所作的不在同一个平面内的三条射线OP,OQ和OR上分别有点P1,P2与点Q1,Q2和R1,R2,则类似的结论为: .
.若从点O所作的不在同一个平面内的三条射线OP,OQ和OR上分别有点P1,P2与点Q1,Q2和R1,R2,则类似的结论为: .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com