[题目]已知函数f(n)=n2sin ).且an=f.则a1+a2+a3+-+a2016的值为题目和参考答案——青夏教育精英家教网—

【题目】已知函数f（n）=n2sin ），且an=f（n）+f（n+1），则a1+a2+a3+…+a2016的值为

【答案】4023
【解析】解：∵f（n）=n2sin ），
∴f（1）=1，f（2）=0，f（3）=﹣32 ， f（4）=0，…，
可得f（2k）=4k2sinkπ=0，k∈N* ， f（2k﹣1）=（2k﹣1）2 =（2k﹣1）2（﹣1）k﹣1 ．
又an=f（n）+f（n+1），
∴a2k﹣1=f（2k﹣1）+f（2k）=（2k﹣1）2（﹣1）k﹣1 ， a2k=f（2k）+f（2k+1）=（2k+1）2（﹣1）k ．
∴a2k﹣1+a2k=（2k﹣1）2（﹣1）k﹣1+（2k+1）2（﹣1）k=（﹣1）k8k．
则a1+a2+a3+…+a2016=8×[﹣1+2﹣3+4+…﹣1007+1008]=4032．﹣．
所以答案是：4032．
【考点精析】本题主要考查了数列的前n项和的相关知识点，需要掌握数列{an}的前n项和sn与通项an的关系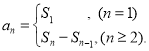才能正确解答此题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】（文科）已知函数.

(1)若，求曲线在点处的切线方程；

(2)若对任意恒成立，求实数的取值范围.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】从某校随机抽取100名学生，获得了他们一周课外阅读时间（单位：小时）的数据，整理得到数据分组及频数分布表和频率分布直方图：

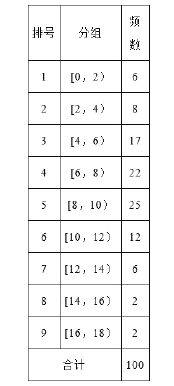
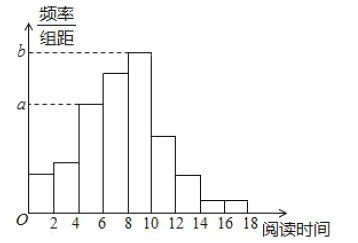
（Ⅰ）从该校随机选取一名学生，试估计这名学生该周课外阅读时间少于12小时的概率；

（Ⅱ）求频率分布直方图中的的值；

（Ⅲ）从阅读时间在的学生中任选2人，求恰好有1人阅读时间在，另1 人阅读时间在的概率.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）在x= 取得最大值2，方程f（x）=0的两个根为x1、x2 ，且|x1﹣x2|的最小值为π．
（1）求f（x）；
（2）将函数y=f（x）图象上各点的横坐标压缩到原来的，纵坐标不变，得到函数y=g（x）的图象，求函数g（x）的单调增区间和在（﹣ ，）上的值域．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】给出20个数，1，2，4，7，11，…，其规律是：第1个数是1，第2个数比第1个数大1，第3个数比第2个数大2，第4个数比第3个数大3，…，以此类推，如图所示的程序框图的功能是计算这20个数的和.

(1)请在程序框图中填写两个（_______）内缺少的内容；

(2)请补充完整该程序框图对应的计算机程序(用WHILE语句编写).

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）= sin2x﹣ cos2x
（1）求f（x）的最小正周期和单调增区间；
（2）若将f（x）的图象上每一点的横坐标伸长到原来的两倍，纵坐标不变，得到函数g（x）的图象，当x∈[ ]时，求函数g（x）的值域．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】2015年年岁史诗大剧《芈月传》风靡大江南北，影响力不亚于以前的《甄嬛传》，某记者调查了大量《芈月传》的观众，发现年龄段与爱看的比例存在较好的线性相关关系，年龄在，，，，的爱看比例分别为，，，，，现用这5个年龄段的中间值代表年龄段，如12代表，17代表，根据前四个数据求得关于爱看比例的线性回归方程为，由此可推测的值为( )