
函数f(x)=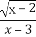 +lg
+lg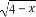 的定义域是( )
的定义域是( )
(A)(2,4) (B)(3,4)
(C)(2,3)∪(3,4] (D)[2,3)∪(3,4)
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试选修4-5不等式选讲练习卷(解析版) 题型:解答题
已知函数f(x)和g(x)的图象关于原点对称,且f(x)=x2+2x.
(1)解关于x的不等式g(x)≥f(x)-|x-1|;
(2)如果对?x∈R,不等式g(x)+c≤f(x)-|x-1|恒成立,求实数c的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试选修4-1几何证明选讲练习卷(解析版) 题型:解答题
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.
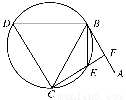
(1)证明:DB=DC;
(2)设圆的半径为1,BC= ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试解答题保分训练练习卷(解析版) 题型:解答题
已知函数f(x)=sin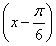 +cos
+cos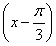 ,g(x)=2sin2
,g(x)=2sin2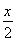 .
.
(1)若α是第一象限角,且f(α)=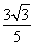 ,求g(α)的值;
,求g(α)的值;
(2)求使f(x)≥g(x)成立的x的取值集合.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(四)第二章第一节练习卷(解析版) 题型:选择题
已知函数y=f(x)的图象关于直线x=-1对称,且当x∈(0,+∞)时,有f(x)=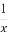 ,则当x∈(-∞,-2)时,f(x)的解析式为( )
,则当x∈(-∞,-2)时,f(x)的解析式为( )
(A)f(x)=-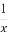 (B)f(x)=-
(B)f(x)=-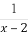
(C)f(x)=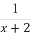 (D)f(x)=-
(D)f(x)=-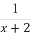
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(六)第二章第三节练习卷(解析版) 题型:解答题
已知函数f(x)=2|x-2|+ax(x∈R)有最小值.
(1)求实数a的取值范围.
(2)设g(x)为定义在R上的奇函数,且当x<0时,g(x)=f(x),求g(x)的解析式.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(六)第二章第三节练习卷(解析版) 题型:选择题
设f(x)是定义在R上以2为周期的偶函数,已知x∈(0,1)时,f(x)=lo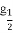 (1-x),则函数f(x)在(1,2)上( )
(1-x),则函数f(x)在(1,2)上( )
(A)是增函数,且f(x)<0
(B)是增函数,且f(x)>0
(C)是减函数,且f(x)<0
(D)是减函数,且f(x)>0
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(八)第二章第五节练习卷(解析版) 题型:选择题
已知函数f(x)=|log2x|,正实数m,n满足m<n,且f(m)=f(n),若f(x)在区间[m2,n]上的最大值为2,则m,n的值分别为( )
(A) ,2 (B)
,2 (B) ,4 (C)
,4 (C)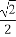 ,
,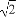 (D)
(D) ,4
,4
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(九)第二章第六节练习卷(解析版) 题型:解答题
已知函数f(x)=3ax2+2bx+c,a+b+c=0,且f(0)·f(1)>0.
(1)求证:-2< <-1.
<-1.
(2)若x1,x2是方程f(x)=0的两个实根,求|x1-x2|的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com