
【题目】已知A,B,C为锐角△ABC的内角, ![]() =(sinA,sinBsinC),
=(sinA,sinBsinC), ![]() =(1,﹣2),
=(1,﹣2), ![]() ⊥
⊥ ![]() .
.
(1)tanB,tanBtanC,tanC能否构成等差数列?并证明你的结论;
(2)求tanAtanBtanC的最小值.
【答案】
(1)解:依题意有sinA=2sinBsinC.
在△ABC中,A=π﹣B﹣C,
所以sinA=sin(B+C)=sinBcosC+cosBsinC,
所以2sinBsinC=sinBcosC+cosBsinC.
因为△ABC为锐角三角形,所以cosB>0,cosC>0,
所以tanB+tanC=2tanBtanC,
所以tanB,tanBtanC,tanC成等差数列
(2)解:在锐角△ABC中,
tanA=tan(π﹣B﹣C)=﹣tan(B+C)=﹣ ![]() ,
,
即tanAtanBtanC=tanA+tanB+tanC,
由(1)知tanB+tanC=2tanBtanC,
于是tanAtanBtanC=tanA+2tanBtanC≥ ![]() ,
,
整理得tanAtanBtanC≥8,
当且仅当tanA=4时取等号,
故tanAtanBtanC的最小值为8
【解析】(1)依题意有sinA=2sinBsinC,从而2sinBsinC=sinBcosC+cosBsinC,再由cosB>0,cosC>0,能推导出tanB,tanBtanC,tanC成等差数列.(2)推导出tanAtanBtanC=tanA+tanB+tanC,从而tanAtanBtanC≥8,由此能求出tanAtanBtanC的最小值为8.


科目:高中数学 来源: 题型:
【题目】一元二次不等式﹣x2+x+2>0的解集是( )
A.{x|x<﹣1或x>2}
B.{x|x<﹣2或x>1}
C.{x|﹣1<x<2}
D.{x|﹣2<x<1}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家庭进行理财投资,根据长期收益率市场调查和预测,投资债券等稳键型产品A的收益与投资成正比,其关系如图1所示;投资股票等风险型产品B的收益与投资的算术平方根成正比,其关系如图2所示(收益与投资单位:万元). 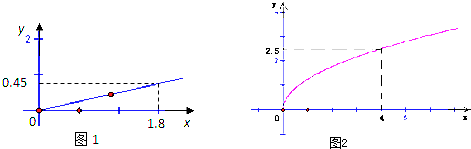
(1)分别将A、B两种产品的收益表示为投资的函数关系式;
(2)该家庭现有10万元资金,并全部投资债券等稳键型产品A及股票等风险型产品B两种产品,问:怎样分配这10万元投资,才能使投资获得最大收益,其最大收益为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=ax2﹣(2a+1)x+a+1对于a∈[﹣1,1]时恒有f(x)<0,则实数x的取值范围是( )
A.(1,2)
B.(﹣∞,1)∪(2,+∞)
C.(0,1)
D.(﹣∞,0)∪(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且a1=2,an+1= ![]() Sn(n=1,2,3,…).
Sn(n=1,2,3,…).
(1)证明:数列{ ![]() }是等比数列;
}是等比数列;
(2)设bn= ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 且Sn=n2﹣4n﹣5.
(1)求数列{an}的通项公式;
(2)设bn=|an|,数列{bn}的前n项和为Tn , 求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln (x+1)-![]() -x,a∈R.
-x,a∈R.
(1)当a>0时,求函数f(x)的单调区间;
(2)若存在x>0,使f(x)+x+1<-![]() (a∈Z)成立,求a的最小值.
(a∈Z)成立,求a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来我国电子商务行业迎来发展的新机遇,与此同时,相关管理部门推出了针对电商商品和服务的评价体系.现从评价系统中选出200次成功交易,并对其评价进行统计,对商品好评率为![]() ,对服务好评率为
,对服务好评率为![]() ,其中对商品和服务都做出好评的交易为80次.
,其中对商品和服务都做出好评的交易为80次.
(1)是否可以在犯错误率不超过0.1%的前提下,认为商品好评与服务好评有关?
(2)若针对商品的好评率,采用分层抽样的方式从这200次交易中取出5次交易,并从中选择两次交易进行客户回访,求只有一次好评的概率.
注:1.
注2. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com