
【题目】已知![]() 的三内角分别为
的三内角分别为![]() ,向量
,向量![]() ,
,![]() ,记函数
,记函数![]() ,
,
(1)若![]() ,求
,求![]() 的面积;
的面积;
(2)若关于![]() 的方程
的方程![]() 有两个不同的实数解,求实数
有两个不同的实数解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
试题(1)由数量积的坐标运算,将![]() 表示为
表示为![]() ,然后利用
,然后利用![]() ,将其转换为关于
,将其转换为关于![]() 的一元函数,并将其变形为
的一元函数,并将其变形为![]() ,计算
,计算![]() 的范围,又
的范围,又![]() ,从而可求出
,从而可求出![]() 的值,进而确定
的值,进而确定![]() ,从而可求
,从而可求![]() 的面积;(2) 方程
的面积;(2) 方程![]() 有两个不同的实数解,即函数
有两个不同的实数解,即函数![]() (
(![]() )的图象和直线
)的图象和直线![]() 有两个不同的交点,为了便于画图象,可设
有两个不同的交点,为了便于画图象,可设![]() ,这样只需画
,这样只需画![]() 的图象和
的图象和![]() 即可,从图象观察,可得实数
即可,从图象观察,可得实数![]() 的取值范围.
的取值范围.
(1)由![]()
即![]() ,
,
又因为![]() ,所以
,所以![]() 代入上式得,
代入上式得,
![]()
由![]() ,得
,得![]() ,
,
又![]() ,所以
,所以![]() ,且
,且![]() 5分
5分
也所以![]() ,即
,即![]() ,从而
,从而![]() 为正三角形,
为正三角形,
所以![]() 8分
8分
(2)由(1)知![]() ,令
,令![]() ,
,
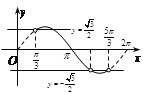
则方程![]() 有两个不同的实数解等价于
有两个不同的实数解等价于![]() 在
在![]() 上有两上不同实根,作出
上有两上不同实根,作出![]() 草图如右,
草图如右,
可知当![]() 或
或![]() 时,直线
时,直线![]() 与曲线
与曲线
![]() 有两个交点,符合题意,故实数
有两个交点,符合题意,故实数![]() 的取值范围为
的取值范围为
![]() . 12分
. 12分


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
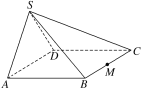
【题目】如图所示,在四棱锥S ABCD中,平面SAD⊥平面ABCD.四边形ABCD为正方形,
(1)求证:CD⊥平面SAD.
(2)若SA=SD,点M为BC的中点,在棱SC上是否存在点N,使得平面DMN⊥平面ABCD?若存在,请说明其位置,并加以证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程为ρ=4cosθ,以极点为原点,极轴为x轴正半轴建立平面直角坐标系,设直线l的参数方程为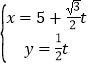 (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程与直线l的普通方程;
(2)设曲线C与直线l相交于P、Q两点,以PQ为一条边作曲线C的内接矩形,求该矩形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于F1 , 焦点为F2;以F1 , F2为焦点,离心率e=![]() 的椭圆C2与抛物线C1在x轴上方的交点为P,延长PF2交抛物线于点Q,M是抛物线C1上一动点,且M在P与Q之间运动.
的椭圆C2与抛物线C1在x轴上方的交点为P,延长PF2交抛物线于点Q,M是抛物线C1上一动点,且M在P与Q之间运动.
当m=1时,求椭圆C2的方程;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,下列说法正确的是____________.
,下列说法正确的是____________.
①函数![]() 的定义域为
的定义域为![]() ;
;
②函数![]() 为奇函数;
为奇函数;
③函数![]() 的值域为
的值域为![]() ;
;
④函数在定义域上为增函数;
⑤对于![]() ,均有
,均有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
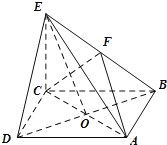
【题目】如图所示,在四棱锥![]() 中,底面ABCD是正方形,AC与BD交于点O,
中,底面ABCD是正方形,AC与BD交于点O,![]() 底面ABCD,F为BE的中点,
底面ABCD,F为BE的中点,![]() .
.
(1)求证:![]() 平面ACF;
平面ACF;
(2)求BE与平面ACE的所成角的正切值;
(3)在线段EO上是否存在点G,使CG![]() 平面BDE ?若存在,求出EG:EO的值,若不存在,请说明理由.
平面BDE ?若存在,求出EG:EO的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cosx(sinx+cosx)﹣![]() .
.
(1)若0<α<![]() , 且sinα=
, 且sinα=![]() , 求f(α)的值;
, 求f(α)的值;
(2)求函数f(x)的最小正周期及单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:kPa)的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组,第二组,![]() ,第五组,右图是根据试验数据制成的频率分布直方图,已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )
,第五组,右图是根据试验数据制成的频率分布直方图,已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )
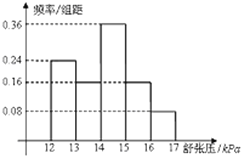
A. 6 B. 8 C. 12 D. 18
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com