
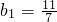 ,bn+1bn=bn+2.数列{an}满足:
,bn+1bn=bn+2.数列{an}满足: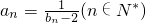
 ,移向整理得an+1+2an+1=0
,移向整理得an+1+2an+1=0
 ∴
∴ 为等比数列
为等比数列 ∴
∴
 ∴
∴
 =
=

 =
=


 ,移向整理即可.
,移向整理即可. ,通过求出
,通过求出 的通项公式,得出{an}的通项公式.
的通项公式,得出{an}的通项公式. ,考虑到(-1)n的取值,宜相邻两项结合,借助放缩法寻求解决.
,考虑到(-1)n的取值,宜相邻两项结合,借助放缩法寻求解决.

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:高中数学 来源: 题型:
| 11 |
| 7 |
| 2 |
| bn |
| 1 |
| bn-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 11 |
| 7 |
| 1 |
| bn-2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省连云港市灌南高级中学高二(上)期中数学模拟试卷(三)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2007-2008学年福建省厦门一中高一(下)期中数学试卷(解析版) 题型:解答题
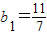 ,
, ,数列{an}满足:
,数列{an}满足: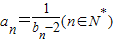 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com