
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() 有两个极值点
有两个极值点![]() ,证明:
,证明:![]() .
.
【答案】(1) 当![]() 时,
时, ![]() 在
在![]() 上单调递增;
上单调递增;
在![]() 上单调递减;
上单调递减;![]() 时,
时, ![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在![]() 上单调递减; 在
上单调递减; 在![]() 上单调递增.
上单调递增.
(2)见解析.
【解析】分析:(1)由![]() ,分别讨论当
,分别讨论当![]() 时,
时,![]() 或
或![]() 讨论导函数的正负从而可得函数的单调性;
讨论导函数的正负从而可得函数的单调性;
(2)由(1)知![]() ,且
,且![]() 为方程
为方程![]() 的两个根,由根与系数的关系
的两个根,由根与系数的关系![]() ,其中
,其中![]() ,可化简
,可化简![]() ,令
,令![]() ,进而求导求最值即可证得.
,进而求导求最值即可证得.
详解:(1) ![]() .
.
令![]() ,
,![]() ,对称轴为
,对称轴为![]() .
.
①当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递增.
上单调递增.
②当![]() 或
或![]() 时,
时,![]() .此时,方程
.此时,方程![]() 两根分别为
两根分别为![]() ,
,![]() .
.
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() ,
,![]() ,所以
,所以![]() 在
在![]() 上单调递增, 在
上单调递增, 在![]() 上单调递减.
上单调递减.
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() ,
,![]() , 所以
, 所以![]() 在
在![]() 上单调递减, 在
上单调递减, 在![]() 上单调递增.
上单调递增.
综上,当![]() 时,
时, ![]() 在
在![]() 上单调递增;
上单调递增;
在![]() 上单调递减;
上单调递减;![]() 时,
时, ![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在![]() 上单调递减; 在
上单调递减; 在![]() 上单调递增.
上单调递增.
(2)由(1)知![]() ,且
,且![]() 为方程
为方程![]() 的两个根.
的两个根.
由根与系数的关系![]() ,其中
,其中![]() .
.
于是![]()
![]() .
.
令![]() ,
,
![]() ,
,
所以在![]() 在
在![]() 上单调递减,且
上单调递减,且![]() .
.
∴![]() ,即
,即![]() ,
,
又![]() ,
,![]() .
.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,
,![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的极值;
的极值;
(Ⅱ)若函数![]() 的两个零点为
的两个零点为![]() ,记
,记![]() ,证明:
,证明:![]() .
.
【答案】(Ⅰ)极大值为![]() ,无极小值;(Ⅱ)证明见解析.
,无极小值;(Ⅱ)证明见解析.
【解析】分析:(Ⅰ)先判断函数![]() 在
在![]() 上的单调性,然后可得当
上的单调性,然后可得当![]() 时,
时,![]() 有极大值,无极小值.(Ⅱ)不妨设
有极大值,无极小值.(Ⅱ)不妨设![]() ,由题意可得
,由题意可得![]() ,即
,即![]() ,又由条件得
,又由条件得![]() ,构造
,构造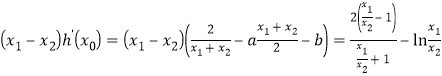 ,令
,令![]() ,则
,则![]() ,利用导数可得
,利用导数可得![]() ,故得
,故得![]() ,又
,又![]() ,所以
,所以![]() .
.
详解:(Ⅰ)![]() ,
,
![]() ,
,
由![]() 得
得![]() ,
,
且当![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上单调递减,
上单调递减,
∴当![]() 时,
时,![]() 有极大值,且
有极大值,且![]() ,无极小值.
,无极小值.
(Ⅱ)![]() 函数
函数![]() 的两个零点为
的两个零点为![]() ,不妨设
,不妨设![]() ,
,
![]() ,
,![]() .
.
![]()
![]() ,
,
即![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,

![]()
![]()
 .
.
令![]() ,则
,则![]()
![]() ,
,
![]() 在
在![]() 上单调递减,
上单调递减,
故![]() ,
,
 ,
,
即![]() ,
,
又![]() ,
,
![]() .
.
点睛:(1)研究方程根的情况,可以通过导数研究函数的单调性、最大(小)值、函数的变化趋势等,根据题目要求,画出函数图象的大体图象,然后通过数形结合的思想去分析问题,可以使得问题的求解有一个清晰、直观的整体展现.
(2)证明不等式时常采取构造函数的方法,然后通过判断函数的单调性,借助函数的最值进行证明.
【题型】解答题
【结束】
22
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ).以坐标原点
).以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,已知曲线
轴正半轴为极轴,建立极坐标系,已知曲线![]() 的极坐标方程为:
的极坐标方程为:![]() .
.
(Ⅰ)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,(其中
,(其中![]() ,
, ![]() 为自然对数的底数,
为自然对数的底数, ![]() ……).
……).
(1)令![]() ,若
,若![]() 对任意的
对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的值;
的值;
(2)在(1)的条件下,设![]() 为整数,且对于任意正整数
为整数,且对于任意正整数![]() ,
, ![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】算筹是在珠算发明以前我国独创并且有效的计算工具,为我国古代数学的发展做出了很大贡献.在算筹计数法中,以“纵式”和“横式”两种方式来表示数字,如图:

表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推,遇零则置空,如图:
![]()
如果把5根算筹以适当的方式全部放入 下面的表格中,那么可以表示的三位数的个数为( )
![]()
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在学年期末举行“我最喜欢的文化课”评选活动,投票规则是一人一票,高一(1)班44名学生和高一(7)班45名学生的投票结果如下表(无废票):
语文 | 数学 | 外语 | 物理 | 化学 | 生物 | 政治 | 历史 | 地理 | |
高一(1)班 | 6 | 9 | 7 | 5 | 4 | 5 | 3 | 3 | 2 |
高一(7)班 |
| 6 |
| 4 | 5 | 6 | 5 | 2 | 3 |
该校把上表的数据作为样本,把两个班同一学科的得票之和定义为该年级该学科的“好感指数”.
(Ⅰ)如果数学学科的“好感指数”比高一年级其他文化课都高,求![]() 的所有取值;
的所有取值;
(Ⅱ)从高一(1)班投票给政治、历史、地理的学生中任意选取![]() 位同学,设随机变量
位同学,设随机变量![]() 为投票给地理学科的人数,求
为投票给地理学科的人数,求![]() 的分布列和期望;
的分布列和期望;
(Ⅲ)当![]() 为何值时,高一年级的语文、数学、外语三科的“好感指数”的方差最小?(结论不要求证明)
为何值时,高一年级的语文、数学、外语三科的“好感指数”的方差最小?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新高考![]() 最大的特点就是取消文理分科,除语文、数学、外语之外,从物理、化学、生物、政治、历史、地理这
最大的特点就是取消文理分科,除语文、数学、外语之外,从物理、化学、生物、政治、历史、地理这![]() 科中自由选择三门科目作为选考科目.某研究机构为了了解学生对全文(选择政治、历史、地理)的选择是否与性别有关,从某学校高一年级的1000名学生中随机抽取男生,女生各
科中自由选择三门科目作为选考科目.某研究机构为了了解学生对全文(选择政治、历史、地理)的选择是否与性别有关,从某学校高一年级的1000名学生中随机抽取男生,女生各![]() 人进行模拟选科.经统计,选择全文的人数比不选全文的人数少
人进行模拟选科.经统计,选择全文的人数比不选全文的人数少![]() 人.
人.

(1)估计在男生中,选择全文的概率.
(2)请完成下面的![]() 列联表;并估计有多大把握认为选择全文与性别有关,并说明理由;
列联表;并估计有多大把握认为选择全文与性别有关,并说明理由;
附: ,其中
,其中![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com