
【题目】某理财公司有两种理财产品A和B.这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立): 产品A产品B(其中p、q>0)
投资结果 | 获利40% | 不赔不赚 | 亏损20% |
概率 |
|
|
|
投资结果 | 获利20% | 不赔不赚 | 亏损10% |
概率 | p |
|
(1)已知甲、乙两人分别选择了产品A和产品B进行投资,如果一年后他们中至少有一人获利的概率大于 ![]() ,求p的取值范围;
,求p的取值范围;
(2)丙要将家中闲置的10万元钱进行投资,以一年后投资收益的期望值为决策依据,在产品A和产品B之中选其一,应选用哪个?
【答案】
(1)解:记事件A为“甲选择产品A且盈利”,
事件B为“乙选择产品B且盈利”,
事件C为“一年后甲、乙两人中至少有一人投资获利”,
则 ![]() ,
,
所以 ![]() ,所以
,所以 ![]() ;
;
又因为 ![]() ,
,
所以 ![]() ;
;
所以 ![]() ;
;
(2)解:假设丙选择产品A进行投资,且记X为获利金额(单位:万元),所以随机变量X的分布列为:
X | 4 | 0 | ﹣2 |
P |
|
|
|
则 ![]() .
.
假设丙选择产品B进行投资,且记Y为获利金额(单位:万元),所以随机变量Y的分布列为:
Y | 2 | 0 | ﹣1 |
P | p |
| q |
则 ![]() ;
;
当 ![]() 时,E(X)=E(Y),选择产品A和产品B一年后投资收益的数学期望相同,可以在产品A和产品B中任选一个;
时,E(X)=E(Y),选择产品A和产品B一年后投资收益的数学期望相同,可以在产品A和产品B中任选一个;
当 ![]() 时,E(X)>E(Y),选择产品A一年后投资收益的数学期望大,应选产品A;
时,E(X)>E(Y),选择产品A一年后投资收益的数学期望大,应选产品A;
当 ![]() 时,E(X)<E(Y),选择产品B一年后投资收益的数学期望大,应选产品B.
时,E(X)<E(Y),选择产品B一年后投资收益的数学期望大,应选产品B.
【解析】(1)利用相互独立事件和对立事件的概率计算公式,求出“甲选择产品A且盈利”、“乙选择产品B且盈利”和“一年后甲、乙两人中至少有一人投资获利”的概率值,列出不等式求出p的取值范围;(2)设丙选择产品A进行投资,记X为获利金额,写出X的分布列,计算数学期望;设丙选择产品B进行投资,记Y为获利金额,写出Y的分布列,计算数学期望;讨论p的取值,得出E(X)与E(Y)的大小关系即可.
【考点精析】利用离散型随机变量及其分布列对题目进行判断即可得到答案,需要熟知在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+a|+|x﹣2|
(1)当a=﹣3时,求不等式f(x)≥3的解集;
(2)若f(x)≤|x﹣4|的解集包含[1,2],求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直角梯形ABCD中,AD∥BC,AD⊥DC,BC=2AD=2DC,四边形ABEF是正方形,且平面ABEF⊥平面ABCD,M为AF的中点, (I)求证:AC⊥BM;
(II)求异面直线CE与BM所成角的余弦值.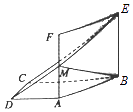
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,内角A,B,C的对边分别为a,b,c,且(c+b)(sinC﹣sinB)=a(sinA﹣sinB).若c=2 ![]() ,则a2+b2的取值范围是 .
,则a2+b2的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1的参数方程为 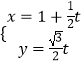 (为参数).在以坐标原点为极点,轴的正半轴为极轴的极坐标系中,曲线C2:
(为参数).在以坐标原点为极点,轴的正半轴为极轴的极坐标系中,曲线C2: ![]() . (Ⅰ)求曲线C1的普通方程和C2的直角坐标方程;
. (Ⅰ)求曲线C1的普通方程和C2的直角坐标方程;
(Ⅱ)若C1与C2相交于A、B两点,设点F(1,0),求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)为奇函数,且在(﹣∞,0)内是减函数,f(﹣2)=0,则xf(x)<0的解集为( )
A.(﹣1,0)∪(2,+∞)
B.(﹣∞,﹣2)∪(0,2)
C.(﹣∞,﹣2)∪(2,+∞)
D.(﹣2,0)∪(0,2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中石化集团获得了某地深海油田区块的开采权,集团在该地区随机初步勘探了部分儿口井,取得了地质资料.进入全面勘探时期后,集团按网络点来布置井位进行全面勘探.由于勘探一口井的费用很高,如果新设计的井位与原有井位重合或接近,便利用旧井的地质资料,不必打这口新井,以节约勘探费用.勘探初期数据资料见如表:
井号I | 1 | 2 | 3 | 4 | 5 | 6 |
坐标(x,y)(km) | (2,30) | (4,40) | (5,60) | (6,50) | (8,70) | (1,y) |
钻探深度(km) | 2 | 4 | 5 | 6 | 8 | 10 |
出油量(L) | 40 | 70 | 110 | 90 | 160 | 205 |
(1)1~6号旧井位置线性分布,借助前5组数据求得回归直线方程为y=6.5x+a,求a,并估计y的预报值;
(2)现准备勘探新井7(1,25),若通过1、3、5、7号井计算出的 ![]() 的值(
的值( ![]() 精确到0.01)相比于(1)中b,a的值之差不超过10%,则使用位置最接近的已有旧井6(1,y),否则在新位置打开,请判断可否使用旧井? (参考公式和计算结果:
精确到0.01)相比于(1)中b,a的值之差不超过10%,则使用位置最接近的已有旧井6(1,y),否则在新位置打开,请判断可否使用旧井? (参考公式和计算结果: 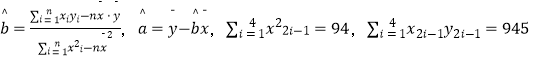 )
)
(3)设出油量与勘探深度的比值k不低于20的勘探并称为优质井,那么在原有井号1~6的出油量不低于50L的井中任意勘探3口井,求恰好2口是优质井的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() =1(a>b>0)的左、右焦点分别为F1 , F2 , 过F2作一条直线(不与x轴垂直)与椭圆交于A,B两点,如果△ABF1恰好为等腰直角三角形,该直线的斜率为( )
=1(a>b>0)的左、右焦点分别为F1 , F2 , 过F2作一条直线(不与x轴垂直)与椭圆交于A,B两点,如果△ABF1恰好为等腰直角三角形,该直线的斜率为( )
A.±1
B.±2
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n(n∈N*)项和为Sn , a3=3,且λSn=anan+1 , 在等比数列{bn}中,b1=2λ,b3=a15+1. (Ⅰ)求数列{an}及{bn}的通项公式;
(Ⅱ)设数列{cn}的前n(n∈N*)项和为Tn , 且 ![]() ,求Tn .
,求Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com