
【题目】命题![]() 方程
方程![]() 表示双曲线;命题
表示双曲线;命题![]() 不等式
不等式![]() 的解集是
的解集是![]() .
. ![]() 为假,
为假, ![]() 为真,求
为真,求![]() 的取值范围.
的取值范围.
【答案】![]()
【解析】试题分析:由命题![]() 方程
方程![]() 表示双曲线,求出
表示双曲线,求出![]() 的取值范围,由命题
的取值范围,由命题![]() 不等式
不等式![]() 的解集是
的解集是![]() ,求出
,求出![]() 的取值范围,由
的取值范围,由![]() 为假,
为假, ![]() 为真,得出
为真,得出![]() 一真一假,分两种情况即可得出
一真一假,分两种情况即可得出![]() 的取值范围.
的取值范围.
试题解析:
![]() 真
真 ![]()
![]() ,
,
![]() 真
真 ![]() 或
或![]()
![]()
∴![]()
![]() 真
真![]() 假
假 ![]()
![]() 假
假![]() 真
真 ![]()
∴![]() 范围为
范围为![]()
【题型】解答题
【结束】
18
【题目】如图,设![]() 是圆
是圆![]() 上的动点,点
上的动点,点![]() 是
是![]() 在
在![]() 轴上的投影,
轴上的投影, ![]() 为
为![]() 上一点,且
上一点,且![]() .
.
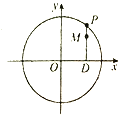
(1)当![]() 在圆上运动时,求点
在圆上运动时,求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)求过点![]() 且斜率为
且斜率为![]() 的直线被
的直线被![]() 所截线段的长度.
所截线段的长度.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某大学餐饮中心为了了解新生的饮食习惯,在某学院大一年级100名学生中进行了抽样调查,发现喜欢甜品的占70%.这100名学生中南方学生共80人.南方学生中有20人不喜欢甜品.
(1)完成下列![]() 列联表:
列联表:
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | |||
北方学生 | |||
合计 |
(2)根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(3)已知在被调查的南方学生中有6名数学系的学生,其中2名不喜欢甜品;有5名物理系的学生,其中1名不喜欢甜品.现从这两个系的学生中,各随机抽取2人,记抽出的4人中不喜欢甜品的人数为X,求X的分布列和数学期望.
附: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥![]() 中,
中,![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,BC//AD,已知Q是四边形ABCD内部一点,且二面角
,BC//AD,已知Q是四边形ABCD内部一点,且二面角![]() 的平面角大小为
的平面角大小为![]() ,若动点Q的轨迹将ABCD分成面积为
,若动点Q的轨迹将ABCD分成面积为![]() 的两部分,则
的两部分,则![]() =_______.
=_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,求:
,求:
(1)过点![]() 与原点距离为2的直线
与原点距离为2的直线![]() 的方程;
的方程;
(2)过点![]() 与原点距离最大的直线
与原点距离最大的直线![]() 的方程,最大距离是多少?
的方程,最大距离是多少?
(3)是否存在过点![]() 与原点距离为6的直线?若存在,求出方程;若不存在,请说明理由.
与原点距离为6的直线?若存在,求出方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了考察冰川的融化状况,一支科考队在某冰川山上相距8km的A、B两点各建一个考察基地,视冰川面为平面形,以过A、B两点的直线为x轴,线段AB的垂直平分线为y轴建立平面直角坐标系(图4).考察范围到A、B两点的距离之和不超过10km的区域.
(I)求考察区域边界曲线的方程:
(II)如图4所示,设线段![]() 是冰川的部分边界线(不考虑其他边界),当冰川融化时,边界线沿与其垂直的方向朝考察区域平行移动,第一年移动0.2km,以后每年移动的距离为前一年的2倍.问:经过多长时间,点A恰好在冰川边界线上?
是冰川的部分边界线(不考虑其他边界),当冰川融化时,边界线沿与其垂直的方向朝考察区域平行移动,第一年移动0.2km,以后每年移动的距离为前一年的2倍.问:经过多长时间,点A恰好在冰川边界线上?
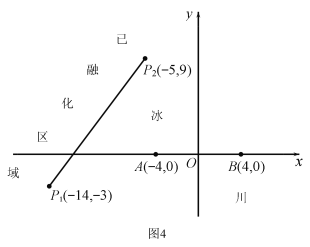
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将![]() 棋盘的每个方格都随意染黑白两色之一,每次操作是将其中同行、同列、同对角线的连续五个方格改变成相反的颜色.试问:能否经过有限次操作,使得所有方格的颜色都变成与原先相反的颜色?
棋盘的每个方格都随意染黑白两色之一,每次操作是将其中同行、同列、同对角线的连续五个方格改变成相反的颜色.试问:能否经过有限次操作,使得所有方格的颜色都变成与原先相反的颜色?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,椭圆上一点
,椭圆上一点![]() 与
与![]() ,
,![]() 的距离之和为
的距离之和为![]() ,且焦距是短轴长的2倍.
,且焦距是短轴长的2倍.
(1)求椭圆的方程;
(2)过线段![]() 上一点的直线
上一点的直线![]() (斜率不为0)与椭圆相交于
(斜率不为0)与椭圆相交于![]() ,
,![]() 两点,当
两点,当![]() 的面积与
的面积与![]() 的面积之比为
的面积之比为![]() 时,求
时,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,离心率为
,离心率为![]() ,过焦点
,过焦点![]() 且垂直于x轴的直线被椭圆C截得的线段长为1.
且垂直于x轴的直线被椭圆C截得的线段长为1.
![]() Ⅰ
Ⅰ![]() 求椭圆C的方程;
求椭圆C的方程;
![]() Ⅱ
Ⅱ![]() 点
点![]() 为椭圆C上一动点,连接
为椭圆C上一动点,连接![]() ,
,![]() ,设
,设![]() 的角平分线PM交椭圆C的长轴于点
的角平分线PM交椭圆C的长轴于点![]() ,求实数m的取值范围.
,求实数m的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 四点均在双曲线
四点均在双曲线![]() 的右支上.
的右支上.
(1)若![]() (实数
(实数![]() ),证明:
),证明:![]() (O是坐标原点);
(O是坐标原点);
(2)若![]() ,P是线段AB的中点,过点P分别作该双曲线的两条渐近线的垂线,垂足为M、N,求四边形
,P是线段AB的中点,过点P分别作该双曲线的两条渐近线的垂线,垂足为M、N,求四边形![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com