
分析 (1)如果共下7盘棋,并且小明与父亲先下,则与父亲下4盘,与母亲下3盘,即可小明恰胜一盘的概率;
(2)如果共下3盘棋,小明与父亲先下,且规定每胜一盘得1分,每负一盘减1分,
ξ的取值为3,1,-1,-3,求出相应的概率,即可求小明最终得分ξ的分布列;
(3)先与父亲下,概率为$\frac{1}{2}$;先与母亲下,概率为$\frac{4}{9}$.
解答 解:(1)如果共下7盘棋,并且小明与父亲先下,则与父亲下4盘,与母亲下3盘
小明恰胜一盘的概率为${C}_{4}^{3}•(\frac{1}{2})^{3}•(\frac{1}{2})•(\frac{1}{3})^{3}$+$(\frac{1}{2})^{4}•{C}_{3}^{1}•\frac{2}{3}•(\frac{1}{3})^{2}$=$\frac{5}{216}$;
(2)如果共下3盘棋,小明与父亲先下,且规定每胜一盘得1分,每负一盘减1分,
ξ的取值为3,1,-1,-3,P(ξ=3)=$\frac{1}{2}•\frac{1}{2}•\frac{2}{3}$=$\frac{1}{6}$,P(ξ=1)=$\frac{1}{2}•\frac{1}{2}•\frac{1}{3}+\frac{1}{2}•\frac{1}{2}•\frac{2}{3}$•2=$\frac{5}{12}$
P(ξ=-1)=$\frac{1}{2}•\frac{1}{2}•\frac{2}{3}$+2$•\frac{1}{2}•\frac{1}{2}•\frac{1}{3}$=$\frac{1}{3}$,P(ξ=-3)=$\frac{1}{2}•\frac{1}{2}•\frac{1}{3}$=$\frac{1}{12}$
∴小明最终得分ξ的分布列
| ξ | 3 | 1 | -1 | -3 |
| P | $\frac{1}{6}$ | $\frac{5}{12}$ | $\frac{1}{3}$ | $\frac{1}{12}$ |
点评 本题考查概率的计算,考查ξ的分布列,考查学生利用数学知识解决实际问题的能力,属于中档题


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
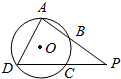 如图,四边形ABCD是⊙O的内接四边形,延长AB和DC相交于点P,若$\frac{PB}{PA}$=$\frac{1}{2}$,$\frac{PC}{PD}$=$\frac{1}{3}$,则$\frac{BC}{AD}$的值为$\frac{\sqrt{6}}{6}$.
如图,四边形ABCD是⊙O的内接四边形,延长AB和DC相交于点P,若$\frac{PB}{PA}$=$\frac{1}{2}$,$\frac{PC}{PD}$=$\frac{1}{3}$,则$\frac{BC}{AD}$的值为$\frac{\sqrt{6}}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2}$] | B. | ($\frac{1}{4}$,$\frac{3}{4}$] | C. | [$\frac{1}{2}$,$\frac{3}{4}$) | D. | [$\frac{1}{4}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com