
【题目】已知圆C:(x﹣3)2+(y﹣4)2=4,直线l过定点A(1,0).
(1)若l与圆C相切,求l的方程;
(2)若l与圆C相交于P、Q两点,若|PQ|=2 ![]() ,求此时直线l的方程.
,求此时直线l的方程.
【答案】
(1)解:若直线l的斜率不存在,则直线l:x=1,符合题意.
若直线l斜率存在,设直线l的方程为y=k(x﹣1),即kx﹣y﹣k=0.
由题意知,圆心(3,4)到已知直线l的距离等于半径2,即: ![]() =2,解之得k=
=2,解之得k= ![]() ,
,
此时直线的方程为3x﹣4y﹣3=0.
综上可得,所求直线l的方程是x=1或3x﹣4y﹣3=0
(2)解:直线与圆相交,斜率必定存在,且不为0,设直线方程为kx﹣y﹣k=0,
因为|PQ|=2 ![]() =2
=2 ![]() =2
=2 ![]() ,求得弦心距d=
,求得弦心距d= ![]() ,
,
即 ![]() =
= ![]() ,求得 k=1或k=7,
,求得 k=1或k=7,
所求直线l方程为x﹣y﹣1=0或7x﹣y﹣7=0
【解析】(1)分直线的斜率存在和不存在两种情况,分别根据直线和圆相切的性质求得直线的方程,综合可得结论.(2)用点斜式设出直线的方程,利用条件以及点到直线的距离公式,弦长公式求出斜率的值,可得直线的方程.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】(12分)
在直角坐标系xOy中,曲线y=x2+mx–2与x轴交于A,B两点,点C的坐标为(0,1).当m变化时,解答下列问题:
(1)能否出现AC⊥BC的情况?说明理由;
(2)证明过A,B,C三点的圆在y轴上截得的弦长为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AD⊥AB,DC∥AB,PA=1,AB=2,PD=BC= ![]() .
. 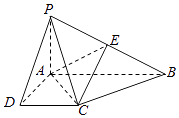
(1)求证:平面PAD⊥平面PCD;
(2)试在棱PB上确定一点E,使截面AEC把该几何体分成的两部分PDCEA与EACB的体积比为2:1;
(3)在(2)的条件下,求二面角E﹣AC﹣P的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,所有棱长均为2,O是底面正方形ABCD中心,E为PC中点,则直线OE与直线PD所成角为( ) 
A.30°
B.60°
C.45°
D.90°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在实数集R上的函数,且y=f(x+1)是偶函数,当x≥1时,f(x)=2x﹣1,则f( ![]() ),f(
),f( ![]() ),f(
),f( ![]() )的大小关系是( )
)的大小关系是( )
A.f( ![]() )<f(
)<f( ![]() )<f(
)<f( ![]() )
)
B.f( ![]() )<f(
)<f( ![]() )<f(
)<f( ![]() )??
)??
C.f( ![]() )<f(
)<f( ![]() )<f(
)<f( ![]() )
)
D.f( ![]() )<f(
)<f( ![]() )<f(
)<f( ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com