
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,右焦点为
,右焦点为![]() ,以原点
,以原点![]() 为圆心,椭圆
为圆心,椭圆![]() 的短半轴长为半径的圆与直线
的短半轴长为半径的圆与直线![]() 相切.
相切.
(1)求椭圆![]() 的方程;
的方程;
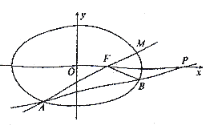
(2)如图,过定点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,连接
两点,连接![]() 并延长交
并延长交![]() 于
于![]() ,求证:
,求证:![]() .
.
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为侧棱
为侧棱![]() 上一点.
上一点.
(Ⅰ)若![]() ,求证:
,求证:![]()
![]() 平面
平面![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)在侧棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出线段
?若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了进一步推动全市学习型党组织、学习型社会建设,某市组织开展“学习强国”知识测试,每人测试文化、经济两个项目,每个项目满分均为60分.从全体测试人员中随机抽取了100人,分别统计他们文化、经济两个项目的测试成绩,得到文化项目测试成绩的频数分布表和经济项目测试成绩的频率分布直方图如下:
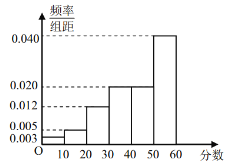
经济项目测试成绩频率分布直方图
分数区间 | 频数 |
| 2 |
| 3 |
| 5 |
| 15 |
| 40 |
| 35 |
文化项目测试成绩频数分布表
将测试人员的成绩划分为三个等级如下:分数在区间![]() 内为一般,分数在区间
内为一般,分数在区间![]() 内为良好,分数在区间
内为良好,分数在区间![]() 内为优秀.
内为优秀.
(1)在抽取的100人中,经济项目等级为优秀的测试人员中女生有14人,经济项目等级为一般或良好的测试人员中女生有34人.填写下面列联表,并根据列联表判断是否有![]() 以上的把握认为“经济项目等级为优秀”与性别有关?
以上的把握认为“经济项目等级为优秀”与性别有关?
优秀 | 一般或良好 | 合计 | |
男生数 | |||
女生数 | |||
合计 |
(2)用这100人的样本估计总体,假设这两个项目的测试成绩相互独立.
(i)从该市测试人员中随机抽取1人,估计其“文化项目等级高于经济项目等级”的概率.
(ii)对该市文化项目、经济项目的学习成绩进行评价.
附:
| 0.150 | 0.050 | 0.010 |
| 2.072 | 3.841 | 6.635 |
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为椭圆
为椭圆![]() 上一点,
上一点,![]() 为椭圆长轴上一点,
为椭圆长轴上一点,![]() 为坐标原点,有下列结论:①存在点
为坐标原点,有下列结论:①存在点![]() ,
,![]() ,使得
,使得![]() 为等边三角形;②不存在点
为等边三角形;②不存在点![]() ,
,![]() ,使得
,使得![]() 为等边三角形;③存在点
为等边三角形;③存在点![]() ,
,![]() ,使得
,使得![]() ;④不存在点
;④不存在点![]() ,
,![]() ,使得
,使得![]() .其中,所有正确结论的序号是( )
.其中,所有正确结论的序号是( )
A.①④B.①③C.②④D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 、
、![]() 两个班共有65名学生,为调查他们的引体向上锻炼情况,通过分层抽样获得了部分学生引体向上的测试数据(单位:个),用茎叶图记录如下:
两个班共有65名学生,为调查他们的引体向上锻炼情况,通过分层抽样获得了部分学生引体向上的测试数据(单位:个),用茎叶图记录如下:
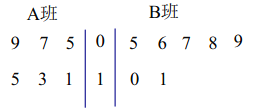
(1)试估计![]() 班的学生人数;
班的学生人数;
(2)从![]() 班和
班和![]() 班抽出的学生中,各随机选取一人,
班抽出的学生中,各随机选取一人,![]() 班选出的人记为甲,
班选出的人记为甲,![]() 班选出的人记为乙,假设所有学生的测试相对独立,比较甲、乙两人的测试数据得到随机变量
班选出的人记为乙,假设所有学生的测试相对独立,比较甲、乙两人的测试数据得到随机变量![]() .规定:当甲的测试数据比乙的测试数据低时,记
.规定:当甲的测试数据比乙的测试数据低时,记![]() ;当甲的测试数据与乙的测试数据相等时,记
;当甲的测试数据与乙的测试数据相等时,记![]() ;当甲的测试数据比乙的测试数据高时,记
;当甲的测试数据比乙的测试数据高时,记![]() .求随机变量
.求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
(3)再从![]() 、
、![]() 两个班中各随机抽取一名学生,他们引体向上的测试数据分别是10,8(单位:个),这2个新数据与表格中的数据构成的新样本的平均数记
两个班中各随机抽取一名学生,他们引体向上的测试数据分别是10,8(单位:个),这2个新数据与表格中的数据构成的新样本的平均数记![]() ,表格中数据的平均数记为
,表格中数据的平均数记为![]() ,试判断
,试判断![]() 和
和![]() 的大小.(结论不要求证明)
的大小.(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在长方体![]() 中,
中,![]() ,点E是棱
,点E是棱![]() 上的一个动点,若平面
上的一个动点,若平面![]() 交棱
交棱![]() 于点
于点![]() ,给出下列命题:
,给出下列命题:
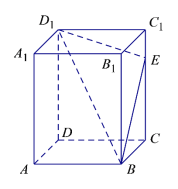
①四棱锥![]() 的体积恒为定值;
的体积恒为定值;
②存在点![]() ,使得
,使得![]() 平面
平面![]() ;
;
③对于棱![]() 上任意一点
上任意一点![]() ,在棱
,在棱![]() 上均有相应的点
上均有相应的点![]() ,使得
,使得![]() 平面
平面![]() ;
;
④存在唯一的点![]() ,使得截面四边形
,使得截面四边形![]() 的周长取得最小值.
的周长取得最小值.
其中真命题的是____________.(填写所有正确答案的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义集合![]() 与集合
与集合![]() 之差是由所有属于
之差是由所有属于![]() 且不属于
且不属于![]() 的元素组成的集合,记作
的元素组成的集合,记作![]() 且
且![]() .已知集合
.已知集合![]() .
.
(Ⅰ)若集合![]() ,写出集合
,写出集合![]() 的所有元素;
的所有元素;
(Ⅱ)从集合![]() 选出10个元素由小到大构成等差数列,其中公差的最大值
选出10个元素由小到大构成等差数列,其中公差的最大值![]() 和最小值
和最小值![]() 分别是多少?公差为
分别是多少?公差为![]() 和
和![]() 的等差数列各有多少个?
的等差数列各有多少个?
(Ⅲ)设集合![]() ,且集合
,且集合![]() 中含有10个元素,证明:集合
中含有10个元素,证明:集合![]() 中必有10个元素组成等差数列.
中必有10个元素组成等差数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com