
【题目】如图,在四棱锥 ![]() 中,
中, ![]() ,且
,且 ![]() .
.
(1)证明:平面 ![]() ⊥平面
⊥平面 ![]() ;
;
(2)若 ![]() ,
, ![]() ,求二面角
,求二面角 ![]() 的余弦值.
的余弦值.
【答案】
(1)解:由已知 ![]() ,得AB⊥AP , CD⊥PD.
,得AB⊥AP , CD⊥PD.
由于AB∥CD , 故AB⊥PD , 从而AB⊥平面PAD.
又AB ![]() 平面PAB , 所以平面PAB⊥平面PAD.
平面PAB , 所以平面PAB⊥平面PAD.
(2)解:在平面 ![]() 内做
内做 ![]() ,垂足为
,垂足为 ![]() ,
,
由(1)可知, ![]() 平面
平面 ![]() ,故
,故 ![]() ,可得
,可得 ![]() 平面
平面 ![]() .
.
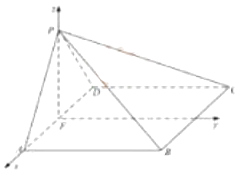
以 ![]() 为坐标原点,
为坐标原点, ![]() 的方向为
的方向为 ![]() 轴正方向,
轴正方向, ![]() 为单位长,建立如图所示的空间直角坐标系
为单位长,建立如图所示的空间直角坐标系 ![]() .
.
由(1)及已知可得 ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
所以 ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
设 ![]() 是平面
是平面 ![]() 的法向量,则
的法向量,则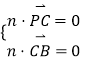 ,即
,即 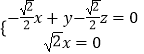 ,
,
可取 ![]() .
.
设 ![]() 是平面
是平面 ![]() 的法向量,则
的法向量,则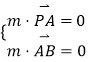 ,即
,即 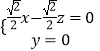 ,
,
可取 ![]() .
.
则 ![]() ,
,
所以二面角 ![]() 的余弦值为
的余弦值为 ![]()
【解析】本题主要考查面面垂直的判定以及利用空间向量求解二面角大小的问题。第一小题主要就是面面垂直判定定理的应用,要正面面面垂直,只要证明面内的一条线垂直于另一个平面即可,也就是要利用线面垂直的判定定理证明即可。第二问建立空间直角坐标系,利用空间向量中的夹角公式求解二面角的大小。


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知 ![]() 在椭圆C:
在椭圆C: ![]() 上,F为右焦点,PF⊥垂直于x轴,A,B,C,D为椭圆上的四个动点,且AC,BD交于原点O.
上,F为右焦点,PF⊥垂直于x轴,A,B,C,D为椭圆上的四个动点,且AC,BD交于原点O.
(1)求椭圆C的方程;
(2)判断直线l: ![]() 与椭圆的位置关系;
与椭圆的位置关系;
(3)设A(x1 , y1),B(x2 , y2)满足 ![]() =
= ![]() ,判断kAB+kBC的值是否为定值,若是,请求出此定值,并求出四边形ABCD面积的最大值,否则说明理由.
,判断kAB+kBC的值是否为定值,若是,请求出此定值,并求出四边形ABCD面积的最大值,否则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在高为2的梯形ABCD中,AB∥CD,AB=2,CD=5,过A、B分别作AE⊥CD,BF⊥CD,垂足分别为E、F.已知DE=1,将梯形ABCD沿AE、BF同侧折起,得空间几何体ADE﹣BCF,如图2. 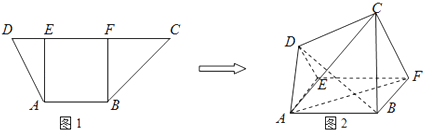
(Ⅰ)若AF⊥BD,证明:△BDE为直角三角形;
(Ⅱ)若DE∥CF, ![]() ,求平面ADC与平面ABFE所成角的余弦值.
,求平面ADC与平面ABFE所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产甲,乙两种产品均需用![]() 两种原料,已知生产1吨每种产品需用
两种原料,已知生产1吨每种产品需用![]() 原料及每天原料的可用限额如下表所示,如果生产1吨甲,乙产品可获利润分别为3万元、4万元,则该企业可获得最大利润为__________万元.
原料及每天原料的可用限额如下表所示,如果生产1吨甲,乙产品可获利润分别为3万元、4万元,则该企业可获得最大利润为__________万元.
甲 | 乙 | 原料限额 | |
A(吨) | 3 | 2 | 12 |
B(吨) | 1 | 2 | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一张坐标纸上涂着圆E: ![]() 及点P(1,0),折叠此纸片,使P与圆周上某点P'重合,每次折叠都会留下折痕,设折痕与直线EP'交于点M .
及点P(1,0),折叠此纸片,使P与圆周上某点P'重合,每次折叠都会留下折痕,设折痕与直线EP'交于点M .
(1)求 ![]() 的轨迹
的轨迹 ![]() 的方程;
的方程;
(2)直线 ![]() 与C的两个不同交点为A , B , 且l与以EP为直径的圆相切,若
与C的两个不同交点为A , B , 且l与以EP为直径的圆相切,若 ![]() ,求△ABO的面积的取值范围.
,求△ABO的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的两个焦点为F1(﹣ ![]() ,0),F2(
,0),F2( ![]() ,0),M是椭圆上一点,若
,0),M是椭圆上一点,若 ![]()
![]() =0,|
=0,| ![]() ||
|| ![]() |=8.
|=8.
(1)求椭圆的方程;
(2)点P是椭圆上任意一点,A1、A2分别是椭圆的左、右顶点,直线PA1 , PA2与直线x= ![]() 分别交于E,F两点,试证:以EF为直径的圆交x轴于定点,并求该定点的坐标.
分别交于E,F两点,试证:以EF为直径的圆交x轴于定点,并求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了引导居民合理用水,某市决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价,具体划分标准如表:
阶梯级别 | 第一阶梯水量 | 第二阶梯水量 | 第三阶梯水量 |
月用水量范围(单位:立方米) | (0,10] | (10,15] | (15,+∞) |
从本市随机抽取了10户家庭,统计了同一个月的用水量,得到如图所示的茎叶图.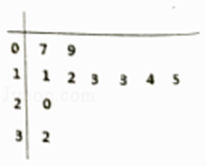
(1)现要在这10户家庭中任意选取3户,求取到第二阶梯水量的户数的分布列和均值;
(2)用抽到的10户家庭作为样本估计全市的居民用水情况,从全市依次随机抽取10户,若抽到n户月用水量为第二阶梯水量的可能性最大,求出n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com